Bài 1.32 trang 32 SBT hình học 10Giải bài 1.32 trang 32 sách bài tập hình học 10. Cho tứ giác ABCD... Quảng cáo
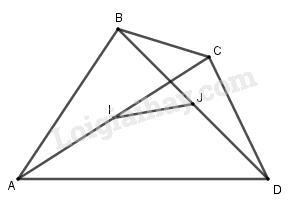
Đề bài Cho tứ giác \(ABCD\). Gọi \(I\) và \(J\) lần lượt là trung điểm của hai đường chéo \(AC\) và \(BD\). Chứng minh \(\overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {IJ} \). Phương pháp giải - Xem chi tiết Xen điểm vào véc tơ \(\overrightarrow {IJ} \) rồi thực hiện cộng các véc tơ. Lời giải chi tiết
Ta có: \(\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AB} + \overrightarrow {BJ} \) \(\overrightarrow {IJ} = \overrightarrow {IC} + \overrightarrow {CD} + \overrightarrow {DJ} \) Cộng từng vế hai đẳng thức trên ta được \(2\overrightarrow {IJ} = \left( {\overrightarrow {IA} + \overrightarrow {IC} } \right) + \left( {\overrightarrow {BJ} + \overrightarrow {DJ} } \right)\)\( + \overrightarrow {AB} + \overrightarrow {CD} \) \( = \overrightarrow {AB} + \overrightarrow {CD} \) Loigiaihay.com  Chia sẻ Bình luận
PH/HS 2K10 Tham Gia Nhóm Zalo Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
|
Danh sách bình luận