Đề kiểm tra 15 phút học kì 1 (lần 1) - Đề số 02Đề bài
Câu 1 :
Chọn phát biểu đúng. Nội dung định luật Ôm là:
Câu 2 :
Khi hiệu điện thế giữa hai đầu dây dẫn tăng thì:
Câu 3 :
Khi đặt vào hai đầu dây dẫn một hiệu điện thế 6V thì cường độ dòng điện qua nó là 0,5A. Nếu hiệu điện thế đặt vào hai đầu dây dẫn là 24V thì cường độ dòng điện qua nó là:
Câu 4 :
Cho đoạn mạch gồm điện trở \({R_1}\) mắc nối tiếp với điện trở \({R_2}\) mắc vào mạch điện. Gọi \(I,{I_1},{I_2}\) lần lượt là cường độ dòng điện của toàn mạch, cường độ dòng điện qua \({R_1},{R_2}\). Biểu thức nào sau đây đúng?
Câu 5 :
Biểu thức nào sau đây xác định điện trở tương đương của đoạn mạch có hai điện trở \({R_1},{R_2}\) mắc nối tiếp?
Câu 6 :
Đặt một hiệu điện thế \({U_{AB}}\) vào hai đầu đoạn mạch gồm hai điện trở \({R_1}\) và \({R_2}\) mắc nối tiếp. Hiệu điện thế giữa hai đầu mỗi điện trở tương ứng là \({U_1},{U_2}\). Hệ thức nào sau đây là không đúng?
Câu 7 :
Sơ đồ mạch điện như hình bên , \({R_1} = 25\Omega \).Biết khi khóa K đóng ampe kế chỉ \(4A\) còn khi khóa K mở thì ampe kế chỉ \(2,5A\). Tính hiệu điện thế giữa hai đầu đoạn mạch và điện trở \({R_2}\)? 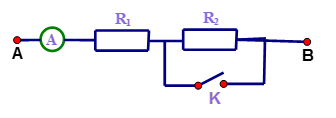
Câu 8 :
Sơ đồ mạch điện như hình bên . Biết \({U_{AE}} = 75{\rm{ }}V,{U_{AC}} = 37,5{\rm{ }}V,{U_{BE}} = 67,5{\rm{ }}V\). Cường độ dòng điện trong mạch có độ lớn \(1,5A\). Điện trở \({R_2}\) có giá trị là: 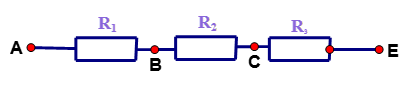
Câu 9 :
Phát biểu nào dưới đây không đúng đối với đoạn mạch gồm các điện trở mắc song song?
Câu 10 :
Biểu thức nào sau đây xác định điện trở tương đương của đoạn mạch có hai điện trở \({R_1},{R_2}\) mắc song song?
Câu 11 :
Đặt một hiệu điện thế \({U_{AB}}\) vào hai đầu đoạn mạch gồm hai điện trở \({R_1}\) và \({R_2}\) mắc song song. Hiệu điện thế giữa hai đầu mỗi điện trở tương ứng là \({U_1},{U_2}\). Hệ thức nào sau đây là đúng?
Câu 12 :
Cho một hiệu điện thế \(U = 1,8V\) và hai điện trở \({R_1},{R_2}\). Nếu mắc nối tiếp hai điện trở vào hiệu điện thế \(U\) thì dòng điện đi qua chúng có cường độ \({I_1} = 0,2{\rm{ }}A\); nếu mắc song song hai điện trở vào hiệu điện thế \(U\) thì dòng điện mạch chính có cường độ \({I_2} = 0,9A\) . Tính \({R_1},{\rm{ }}{R_2}\)?
Lời giải và đáp án
Câu 1 :
Chọn phát biểu đúng. Nội dung định luật Ôm là:
Đáp án : C Lời giải chi tiết :
Cường độ dòng điện qua dây dẫn tỷ lệ thuận với hiệu điện thế đặt vào hai đầu dây và tỷ lệ nghịch với điện trở của dây
Câu 2 :
Khi hiệu điện thế giữa hai đầu dây dẫn tăng thì:
Đáp án : D Lời giải chi tiết :
Ta có: Cường độ dòng điện qua dây dẫn tỷ lệ thuận với hiệu điện thế đặt vào hai đầu dây và tỷ lệ nghịch với điện trở của dây$I = \frac{U}{R}$ => khi hiệu điện thế giữa hai đầu dây dẫn tăng thì cường độ dòng điện chạy qua dây dẫn tăng tỉ lệ với hiệu điện thế.
Câu 3 :
Khi đặt vào hai đầu dây dẫn một hiệu điện thế 6V thì cường độ dòng điện qua nó là 0,5A. Nếu hiệu điện thế đặt vào hai đầu dây dẫn là 24V thì cường độ dòng điện qua nó là:
Đáp án : B Lời giải chi tiết :
Ta có , điện trở dây dẫn là không thay đổi. Áp dụng biểu thức định luật Ôm:$I = \dfrac{U}{R}$ , ta có: + Khi hiệu điện thế đặt vào hai đầu dây dẫn là \({U_1} = 6V\) thì: ${I_1} = \dfrac{{{U_1}}}{R} \to R = \dfrac{{{U_1}}}{{{I_1}}} = \dfrac{6}{{0,5}} = 12\Omega $ + Khi hiệu điện thế đặt vào hai đầu dây dẫn là ${U_2} = 24V$, khi đó: ${I_2} = \dfrac{{{U_2}}}{R} = \dfrac{{24}}{{12}} = 2{\text{A}}$
Câu 4 :
Cho đoạn mạch gồm điện trở \({R_1}\) mắc nối tiếp với điện trở \({R_2}\) mắc vào mạch điện. Gọi \(I,{I_1},{I_2}\) lần lượt là cường độ dòng điện của toàn mạch, cường độ dòng điện qua \({R_1},{R_2}\). Biểu thức nào sau đây đúng?
Đáp án : A Lời giải chi tiết :
Ta có, trong đoạn mạch mắc nối tiếp thì: Cường độ dòng điện có giá trị như nhau tại mọi điểm: \(I = {I_1} = {I_2} = \ldots = {I_n}\)
Câu 5 :
Biểu thức nào sau đây xác định điện trở tương đương của đoạn mạch có hai điện trở \({R_1},{R_2}\) mắc nối tiếp?
Đáp án : C Lời giải chi tiết :
Ta có: Điện trở tương đương của đoạn mạch nối tiếp bằng tổng các điện trở hợp thành: \({R_{td}} = {R_1} + {R_2}\)
Câu 6 :
Đặt một hiệu điện thế \({U_{AB}}\) vào hai đầu đoạn mạch gồm hai điện trở \({R_1}\) và \({R_2}\) mắc nối tiếp. Hiệu điện thế giữa hai đầu mỗi điện trở tương ứng là \({U_1},{U_2}\). Hệ thức nào sau đây là không đúng?
Đáp án : C Lời giải chi tiết :
A, B, D - đúng C - sai vì: \(\frac{{{U_1}}}{{{U_2}}} = \frac{{{R_1}}}{{{R_2}}}\) do \(I = \frac{U}{R}\) mà \(I = {I_1} = {I_2} \to \frac{{{U_1}}}{{{R_1}}} = \frac{{{U_2}}}{{{R_2}}} \to \frac{{{U_1}}}{{{U_2}}} = \frac{{{R_1}}}{{{R_2}}}\)
Câu 7 :
Sơ đồ mạch điện như hình bên , \({R_1} = 25\Omega \).Biết khi khóa K đóng ampe kế chỉ \(4A\) còn khi khóa K mở thì ampe kế chỉ \(2,5A\). Tính hiệu điện thế giữa hai đầu đoạn mạch và điện trở \({R_2}\)? 
Đáp án : A Phương pháp giải :
+ Vận dụng biểu thức tính hiệu điện thế: \(U = IR\) + Áp dụng biểu thức tính điện trở tương đương trong đoạn mạch mắc nối tiếp: \(R = {R_1} + {R_2}\) Lời giải chi tiết :
- Khi khóa K đóng thì dòng điện không đi qua điện trở \({R_2}\), nên số chỉ của ampe kế là số chỉ cường độ dòng điện chạy trong mạch Hiệu điện thế hai đầu đoạn mạch là : \(U = I{R_1} = 4.25 = 100V\) - Khi khóa K mở , hai điện trở \({R_1}\) và \({R_2}\) mắc nối tiếp , nên điện trở của đoạn mạch là: \({R_{12}} = \frac{U}{I} = \frac{{100}}{{2,5}} = 40\Omega \) Điện trở \({R_2} = {R_{12}}-{R_1} = 40-25 = 15\Omega \)
Câu 8 :
Sơ đồ mạch điện như hình bên . Biết \({U_{AE}} = 75{\rm{ }}V,{U_{AC}} = 37,5{\rm{ }}V,{U_{BE}} = 67,5{\rm{ }}V\). Cường độ dòng điện trong mạch có độ lớn \(1,5A\). Điện trở \({R_2}\) có giá trị là: 
Đáp án : B Phương pháp giải :
+ Áp dụng biểu thức tính điện trở: \(R = \frac{U}{I}\) + Vận dụng biểu thức tính điện trở tương đương của đoạn mạch mắc nối tiếp: \(R = {R_1} + {R_2} + ...\) Lời giải chi tiết :
+ Điện trở của đoạn mạch \({R_{AC}} = \dfrac{{{U_{AC}}}}{I} = \dfrac{{37,5}}{{1,5}} = 25\Omega \) \({R_{AE}} = \dfrac{{{U_{AE}}}}{{I{\rm{ }}}} = \dfrac{{75}}{{1,5}} = 50\Omega\) \({R_{BE}} = \dfrac{{{U_{BE}}}}{I} = \dfrac{{67,5}}{{1,5}} = 45\Omega \) + Mà \(\left\{ \begin{array}{l}{R_{AE}} = {R_1} + {R_2} + {R_3} = 50\Omega \\{\rm{ }}{R_{AC}} = {R_1} + {R_2} = 25\Omega \\{R_{BE}} = {R_2} + {R_3} = 45\Omega \end{array} \right.\) Vậy suy ra: \({R_1} = 5\Omega ;{R_3} = 25\Omega ;{R_2} = 20\Omega \)
Câu 9 :
Phát biểu nào dưới đây không đúng đối với đoạn mạch gồm các điện trở mắc song song?
Đáp án : B Lời giải chi tiết :
A, C, D - đúng B - sai vì: Hiệu điện thế hai đầu đoạn mạch song song bằng hiệu điện thế hai đầu mỗi đoạn mạch rẽ: \(U = {U_1} = {U_2} = \ldots = {U_n}\)
Câu 10 :
Biểu thức nào sau đây xác định điện trở tương đương của đoạn mạch có hai điện trở \({R_1},{R_2}\) mắc song song?
Đáp án : A Lời giải chi tiết :
Ta có: Nghịch đảo điện trở tương đương của đoạn mạch song song bằng tổng các nghịch đảo điện trở các đoạn mạch rẽ: $\frac{1}{{{R_{t{\text{d}}}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}$
Câu 11 :
Đặt một hiệu điện thế \({U_{AB}}\) vào hai đầu đoạn mạch gồm hai điện trở \({R_1}\) và \({R_2}\) mắc song song. Hiệu điện thế giữa hai đầu mỗi điện trở tương ứng là \({U_1},{U_2}\). Hệ thức nào sau đây là đúng?
Đáp án : C Lời giải chi tiết :
A - sai vì: \(\frac{1}{{{R_{AB}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\) B - sai vì: \({I_{A{\bf{B}}}} = {I_1} + {I_2}\) C - đúng D - sai \({U_{AB}} = {U_1} = {U_2}\)
Câu 12 :
Cho một hiệu điện thế \(U = 1,8V\) và hai điện trở \({R_1},{R_2}\). Nếu mắc nối tiếp hai điện trở vào hiệu điện thế \(U\) thì dòng điện đi qua chúng có cường độ \({I_1} = 0,2{\rm{ }}A\); nếu mắc song song hai điện trở vào hiệu điện thế \(U\) thì dòng điện mạch chính có cường độ \({I_2} = 0,9A\) . Tính \({R_1},{\rm{ }}{R_2}\)?
Đáp án : A Phương pháp giải :
+ Sử dụng biểu thức tính tổng trở của đoạn mạch mắc nối tiếp: \({R_{nt}} = {R_1} + {R_2}\) + Sử dụng biểu thức tính tổng trở của đoạn mạch mắc song song: \(\frac{1}{{{R_{//}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}\) Lời giải chi tiết :
+ Khi \({R_1},{R_2}\) mắc nối tiếp nên \({R_1} + {R_2} = \dfrac{U}{{{I_1}}} = \dfrac{{1,8}}{{0,2}} = 9\Omega \) (1) + Khi \({R_1},{R_2}\) mắc song song nên \({R_{12}} = \dfrac{U}{{{I_2}}} = \dfrac{{1,8}}{{0,9}} = 2\Omega \), mà \({{\rm{R}}_{{\rm{12}}}} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\) Cho nên \({R_1}{R_2} = 18\) (2) Từ (1) ta có \({R_2} = 9-{R_1}\) thay vào (2) ta có : \(\begin{array}{l}{R_1}\left( {9{\rm{ }}-{\rm{ }}{R_1}} \right) = 18\\ \leftrightarrow {R_1}^2 - 9R_1+18 =0 \leftrightarrow \left( {{R_1}-3} \right)\left( {{R_1}-6} \right) = 0\end{array}\) \(\left[ \begin{array}{l}{R_1} = 3\Omega \\{R_2} = 6\Omega \end{array} \right. \Rightarrow \left[ \begin{array}{l}{R_2} = 9 - 3 = 6\Omega \\{R_2} = 9 - 6 = 3\Omega \end{array} \right.\) Vậy \({R_1} = 3\Omega ;{R_2} = 6\Omega \) hoặc \({R_1} = 6\Omega ;{R_2} = 3\Omega \) |




















Danh sách bình luận