Trắc nghiệm Bài 59: Rút gọn phân số Toán 4 Cánh diềuĐề bài
Câu 1 :
Trong các phân số sau, phân số nào là phân số tối giản? A. \(\dfrac{6}{9}\) B. \(\dfrac{4}{7}\) C. \(\dfrac{{20}}{{15}}\) D. \(\dfrac{{15}}{{27}}\)
Câu 2 :
Rút gọn phân số sau thành phân số tối giản: $\frac{5}{20}=\frac{?}{?}$
Câu 3 :
\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai? A. Đúng B. Sai
Câu 6 :
Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là: A. \(\dfrac{2}{5}\) B. \(\dfrac{3}{5}\) C. \(\dfrac{{18}}{{45}}\) D. \(\dfrac{8}{{20}}\)
Câu 7 :
Rút gọn phân số sau thành phân số tối giản: $\frac{2\times 9\times 44}{33\times 45\times 7}=\frac{?}{?}$
Câu 8 :
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số $\frac{?}{?}$
Lời giải và đáp án
Câu 1 :
Trong các phân số sau, phân số nào là phân số tối giản? A. \(\dfrac{6}{9}\) B. \(\dfrac{4}{7}\) C. \(\dfrac{{20}}{{15}}\) D. \(\dfrac{{15}}{{27}}\) Đáp án
B. \(\dfrac{4}{7}\) Phương pháp giải :
- Rút gọn các phân số đã cho (nếu được) Lời giải chi tiết :
Ta có: \(\dfrac{6}{9} = \dfrac{{6:3}}{{9:3}} = \dfrac{2}{3}\,\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{20}}{{15}} = \dfrac{{20:5}}{{15:5}} = \dfrac{4}{3}\,\,\, ;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{15}}{{27}} = \dfrac{{15:3}}{{27:3}} = \dfrac{5}{9}\) Phân số \(\dfrac{4}{7}\) có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn \(1\), nên \(\dfrac{4}{7}\) là phân số tối giản. Vậy trong các phân số đã cho, phân số tối giản là phân số \(\dfrac{4}{7}\).
Câu 2 :
Rút gọn phân số sau thành phân số tối giản: $\frac{5}{20}=\frac{?}{?}$
Đáp án
$\frac{5}{20}=\frac{1}{4}$
Phương pháp giải :
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta chia cả tử số và mẫu số của phân số \(\dfrac{5}{{20}}\) cho \(5\). Lời giải chi tiết :
Ta thấy \(5\) và \(20\) cùng chia hết cho \(5\) nên ta có: \(\dfrac{5}{{20}} = \dfrac{{5:5}}{{20:5}} = \dfrac{1}{4}\) Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(1\,;\,\,4\).
Câu 3 :
\(\dfrac{{4 \times 5 \times 7}}{{7 \times 5 \times 9}} = \dfrac{4}{9}\) . Đúng hay sai? A. Đúng B. Sai Đáp án
A. Đúng B. Sai Phương pháp giải :
Tích ở tử số và mẫu số đều có thừa số chung là \(5\) và \(7\) nên ta cùng chia nhẩm tích ở tử số và mẫu số cho \(5\), rồi cùng chia nhẩm cho \(7\). Lời giải chi tiết :
Ta có:
Vậy phép tính đã cho là đúng.
Đáp án : B Phương pháp giải :
Phân số tối giản là phân số có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1. Lời giải chi tiết :
Phân số chưa tối giản là $\frac{{21}}{{35}}$
Đáp án : A Phương pháp giải :
Rút gọn phân số đã cho để trả lời câu hỏi của bài toán Lời giải chi tiết :
Ta có $\frac{{24}}{{120}} = \frac{1}{5} = \frac{{20}}{{100}}$
Câu 6 :
Rút gọn phân số \(\dfrac{{72}}{{180}}\) ta được phân số tối giản là: A. \(\dfrac{2}{5}\) B. \(\dfrac{3}{5}\) C. \(\dfrac{{18}}{{45}}\) D. \(\dfrac{8}{{20}}\) Đáp án
A. \(\dfrac{2}{5}\) Phương pháp giải :
Khi rút gọn phân số có thể làm như sau: - Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\). - Chia tử số và mẫu số cho số đó. Cứ làm như thế cho đến khi nhận được phân số tối giản. Lời giải chi tiết :
Ta thấy phân số \(\dfrac{{72}}{{180}}\) có tử số và mẫu số đều chia hết cho \(4\), nên ta có: \(\dfrac{{72}}{{180}} = \dfrac{{72:4}}{{180:4}} = \dfrac{{18}}{{45}}\) Ta thấy phân số \(\dfrac{{18}}{{45}}\) có tử số và mẫu số đều chia hết cho \(9\), nên ta có: \(\dfrac{{18}}{{45}} = \dfrac{{18:9}}{{45:9}} = \dfrac{2}{5}\) Ta thấy phân số \(\dfrac{2}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{2}{5}\) là phân số tối giản. Vậy \(\dfrac{{72}}{{180}} = \dfrac{2}{5}\). Chú ý
Ta thấy hai phân số \(\dfrac{{18}}{{45}}\) và \(\dfrac{8}{{20}}\) đều bằng phân số \(\dfrac{{72}}{{180}}\), tuy nhiên hai phân số đó chưa phải là phân số tối giản nên hai đáp án C, D chưa đúng.
Câu 7 :
Rút gọn phân số sau thành phân số tối giản: $\frac{2\times 9\times 44}{33\times 45\times 7}=\frac{?}{?}$
Đáp án
$\frac{2\times 9\times 44}{33\times 45\times 7}=\frac{8}{105}$
Phương pháp giải :
Phân tích tử số và mẫu số thành tích của các thừa số, sau đó chia nhẩm tích ở tử số và mẫu số cho các thừa số chung. Lời giải chi tiết :
Tách \(44\) thành tích của \(11\) và \(4\), tách \(33\) thành tích của \(11\) và \(3\) , tách \(45\) thành tích của \(9\) và \(5\) , ta có: \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{{2 \times 9 \times 11 \times 4}}{{11 \times 3 \times 9 \times 5 \times 7}}\) Ta thấy tích ở trên gạch ngang và tích ở dưới gạch ngang đều có chung các thừa số là \(9\) và \(11\). Cùng chia nhẩm tích ở trên gạch ngang và tích ở dưới gạch ngang cho \(9\) và \(11\) ta được: Mà \(\dfrac{8}{{105}}\) là phân số tối giản vì có tử số và mẫu số không cùng chia hết cho số tự nhiên nào khác \(1\). Vậy \(\dfrac{{2 \times 9 \times 44}}{{33 \times 45 \times 7}} = \dfrac{8}{{105}}\) Đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(8\,;\,\,105\).
Câu 8 :
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số $\frac{?}{?}$
Đáp án
$\frac{3}{5}$
Phương pháp giải :
Phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\). Lời giải chi tiết :
Phân số cần tìm bằng phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất chính là phân số tối giản sau khi rút gọn phân số \(\dfrac{{216}}{{360}}\). Rút gọn phân số \(\dfrac{{216}}{{360}}\) để được phân số tối giản, ta có: \(\begin{array}{l}\dfrac{{216}}{{360}} = \dfrac{{216:4}}{{360:4}} = \dfrac{{54}}{{90}}\\\dfrac{{54}}{{90}} = \dfrac{{54:9}}{{90:9}} = \dfrac{6}{{10}}\\\dfrac{6}{{10}} = \dfrac{{6:2}}{{10:2}} = \dfrac{3}{5}\end{array}\) Ta thấy phân số \(\dfrac{3}{5}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn \(1\) nên \(\dfrac{3}{5}\) là phân số tối giản. Do đó, phân số bằng với phân số \(\dfrac{{216}}{{360}}\) và có mẫu số bé nhất là phân số \(\dfrac{3}{5}\). Vậy đáp án đúng điền vào ô trống lần lượt từ trên xuống dưới là \(3\,;\,\,5\).
|















.jpg)






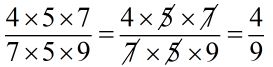





Danh sách bình luận