Lý thuyết Ứng dụng hình học của tích phân Toán 12 Chân trời sáng tạo

1.Tính diện tích hình phẳng

a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b

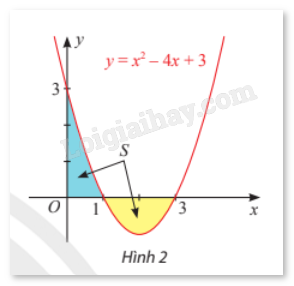
Nếu hàm số \(y = f(x)\) không đổi dấu trên đoạn [a;b] thì \(S = \int\limits_a^b {\left| {f(x)} \right|dx}  = \left| {\int\limits_a^b {f(x)dx} } \right|\).

Đặc biệt, nếu phương trình \(f(x) = 0\) không có nghiệm trên khoảng (a;b) thì công thức trên vẫn đúng.

Nếu phương trình \(f(x) = 0\) chỉ có một nghiệm c trên khoảng (a;b) thì \(S = \left| {\int\limits_a^c {f(x)dx} } \right| + \left| {\int\limits_c^b {f(x)dx} } \right|\).

Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f(x) = {x^2} - 4x + 3\), trục hoành và hai đường thẳng x = 0, x = 3.

Giải: Diện tích cần tìm là \(S = \int\limits_0^3 {\left| {{x^2} - 4x + 3} \right|dx} \).

Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \) x = 1 hoặc x = 3.

Với \(x \in \left[ {0;1} \right]\) thì \(f(x) \ge 0\). Với \(x \in \left[ {1;3} \right]\) thì \(f(x) \le 0\).

Vậy \(S = \int\limits_0^3 {\left| {{x^2} - 4x + 3} \right|dx}  = \int\limits_0^1 {\left( {{x^2} - 4x + 3} \right)dx}  + \int\limits_1^3 {\left[ { - \left( {{x^2} - 4x + 3} \right)} \right]dx} \)

\( = \left( {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right)\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right. - \left( {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right)\left| {\begin{array}{*{20}{c}}3\\1\end{array}} \right. = \frac{8}{3}\).

b) Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b

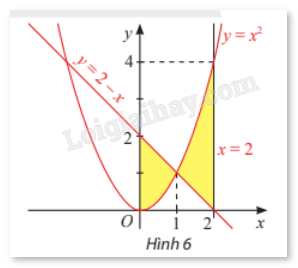
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2}\), \(y = 2 - x\) và hai đường thẳng x = 0, x = 2.

Giải: Diện tích cần tìm là \(\int\limits_0^2 {\left| {{x^2} - (2 - x)} \right|dx}  = \int\limits_0^2 {\left| {{x^2} + x - 2} \right|dx} \).

Ta có \({x^2} + x - 2 = 0 \Leftrightarrow \) x = 1 hoặc x = -2.

Vậy \(S = \int\limits_0^1 {\left| {{x^2} + x - 2} \right|dx}  + \int\limits_1^2 {\left| {{x^2} + x - 2} \right|dx}  = \left| {\int\limits_0^1 {\left( {{x^2} + x - 2} \right)dx} } \right| + \left| {\int\limits_1^2 {\left( {{x^2} + x - 2} \right)dx} } \right|\)

\( = \left| {\left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x} \right)\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right.} \right| + \left| {\left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right.} \right| = \left| { - \frac{7}{6}} \right| + \left| {\frac{{11}}{6}} \right| = 3\).

2. Tính thể tích của hình khối

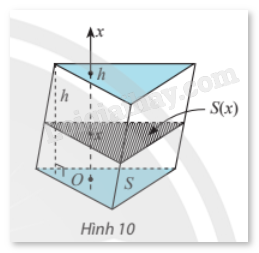
Ví dụ: Cho khối lăng trụ tam giác có diện tích đáy S và chiều cao h. Sử dụng tích phân, tính thể tích của khối lăng trụ theo S và h.

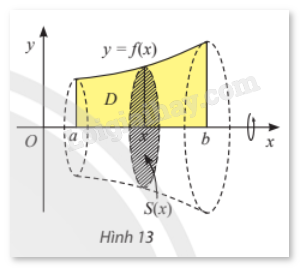
Giải: Chọn trục Ox song song với đường cao của khối lăng trụ sao cho hai đáy nằm trong hai mặt phẳng vuông góc với Ox tại x = 0 và x = h.

Mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \((0 \le x \le h)\) cắt lăng trụ theo mặt cắt có diện tích không đổi S(x) = S. Do đó, thể tích khối lăng trụ là \(V = \int\limits_0^h {S(x)dx}  = \int\limits_0^h {Sdx}  = Sx\left| {\begin{array}{*{20}{c}}h\\0\end{array}} \right. = Sh\).

3. Thể tích khối tròn xoay

Cho \(y = f(x)\) là hàm số liên tục và không âm trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục hoành và hai đường thẳng x = a, x = b.

Quay D quanh trục Ox ta được một hình khối gọi là khối tròn xoay.

Cắt khối tròn xoay trên bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x với \(x \in [a;b]\), ta được mặt cắt là hình tròn có bán kính bằng \(f(x)\) và diện tích là \(S(x) = \pi {f^2}(x)\).