Giải mục 2 trang 24, 25, 26 SGK Toán 12 tập 2 - Chân trời sáng tạoTính thể tích hình khối Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
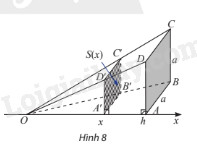
KP3 Trả lời câu hỏi Khám phá 3 trang 24 SGK Toán 12 Chân trời sáng tạo Trong không gian, cho hình chóp \(O.ABCD\) có đáy là hình vuông cạnh \(a\), \(OA \bot \left( {ABCD} \right)\), \(OA = h\). Đặt trục số \(Ox\) như Hình 8. Một mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 < x \le h} \right)\), cắt hình chóp \(O.ABCD\) theo mặt cắt là hình vuông \(A'B'C'D'\). Kí hiệu \(S\left( x \right)\) là diện tích của hình vuông \(A'B'C'D'\).
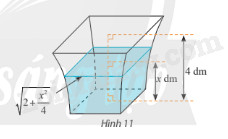
a) Tính \(S\left( x \right)\) theo \(a\), \(h\) và \(x\). b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và so sánh với thể tích của khối chóp \(O.ABCD\). Phương pháp giải: a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\). Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}}\), từ đó tính được \(A'D'\), sau đó tính \(S\left( x \right)\). b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và thể tích khối chóp \(O.ABCD\) và so sánh các kết quả với nhau. Lời giải chi tiết: a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\). Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}} \Rightarrow A'D' = \frac{{OA'.AD}}{{OA}} = \frac{{x.a}}{h}\) Suy ra \(S\left( x \right) = A'D{'^2} = {\left( {\frac{{x.a}}{h}} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\) b) Ta có: \(\int\limits_0^h {S\left( x \right)dx} = \frac{{{a^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\) Thể tích khối chóp \(O.ABCD\) là \({V_{O.ABCD}} = \frac{1}{3}.{a^2}.h = \frac{{{a^2}h}}{3}\) Như vậy \({V_{O.ABCD}} = \int\limits_0^h {S\left( x \right)dx} \) TH5 Trả lời câu hỏi Thực hành 5 trang 25 SGK Toán 12 Chân trời sáng tạo Một bình chứa nước có dạng như hình 11. Biết rằng khi nước ở trong bình có chiều cao \(x\) (dm) \(\left( {0 \le x \le 4} \right)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} \) (dm). Tính dung tích của bình.
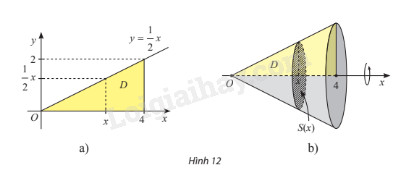
Phương pháp giải: Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\). Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\). Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} \). Lời giải chi tiết: Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\). Diện tích mặt nước ở chiều cao \(x\) là: \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\). Dung tích của bình là: \(V = \int\limits_0^4 {S\left( x \right)dx} = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx} = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\). KP4 Trả lời câu hỏi Khám phá 4 trang 25 SGK Toán 12 Chân trời sáng tạo Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{1}{2}x\), trục hoành và đường thẳng \(x = 4\) (Hình 12a). Quay hình \(D\) xung quanh trục \(Ox\) thì được một khối nón, kí hiệu là \(N\) (Hình 12b). a) Cắt khối \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le 4} \right)\) thì mặt cắt là hình gì? Tính diện tích \(S\left( x \right)\) của mặt cắt đó. b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón \(N\).
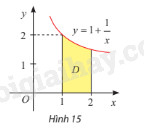
Phương pháp giải: a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Tính bán kính của hình tròn, từ đó tính được diện tích \(S\left( x \right)\) của mặt cắt đó. b) Công thức tính thể tích của khối nón \(N\) có bán kính đáy \(r\) và chiều cao \(h\): \(V = \frac{1}{3}\pi {r^2}h\). Lời giải chi tiết: a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Ta nhận thấy rằng khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) thì bán kính mặt cắt sẽ là \(\frac{1}{2}x\). Do đó diện tích của mặt cắt là \(S\left( x \right) = \pi .{\left( {\frac{1}{2}x} \right)^2} = \frac{\pi }{2}{x^2}\). b) Khối nón \(N\) có bán kính đáy \(r = 2\) và chiều cao \(h = 4\) nên thể tích của khối nón là: \(V = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\). TH6 Trả lời câu hỏi Thực hành 6 trang 26 SGK Toán 12 Chân trời sáng tạo Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 1 + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) (Hình 15). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
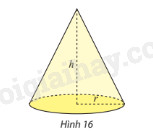
Phương pháp giải: Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\), với \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\), là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \). Lời giải chi tiết: Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) là: \(V = \pi \int\limits_1^2 {{{\left( {1 + \frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {\left( {1 + \frac{2}{x} + \frac{1}{{{x^2}}}} \right)dx} \) \(= \pi \left. {\left( {x + 2\ln \left| x \right| - \frac{1}{x}} \right)} \right|_1^2 = \pi \left( {\frac{3}{2} + 2\ln 2} \right)\). VD2 Trả lời câu hỏi Vận dụng 2 trang 27 SGK Toán 12 Chân trời sáng tạo Sử dụng tích phân, tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\) (Hình 16).
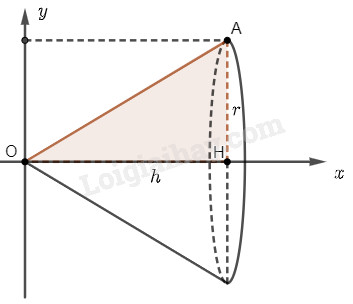
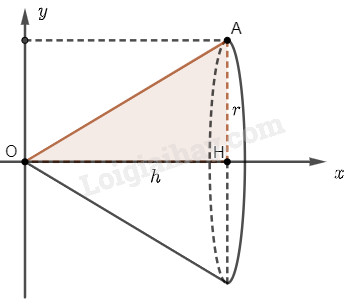
Phương pháp giải:
Chọn trục \(Ox\) và \(Oy\) như hình vẽ. Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\). Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\). Thể tích của khối nón là \(V = \pi \int\limits_0^h {{f^2}\left( x \right)dx} \). Lời giải chi tiết:
Chọn trục \(Ox\) và \(Oy\) như hình vẽ. Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\). Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\). Đường thẳng \(OA\) đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {h;r} \right)\) nên phương trình đường thẳng \(OA\) là \(y = \frac{r}{h}x\). Thể tích khối nón là: \(V = \pi \int\limits_0^h {{{\left( {\frac{r}{h}x} \right)}^2}dx} = \pi \frac{{{r^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} \) \(= \frac{{\pi {r^2}}}{{{h^2}}}.\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{\pi {r^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{\pi {r^2}h}}{3}\).
|




















Danh sách bình luận