Lý thuyết Tỉ số lượng giác của góc nhọn Toán 9 Kết nối tri thức1. Khái niệm tỉ số lượng giác của một góc nhọn Quảng cáo
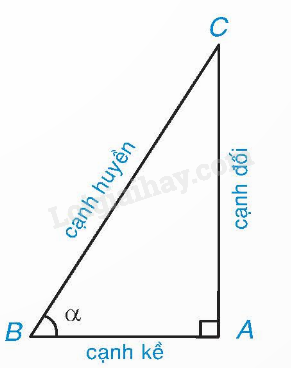
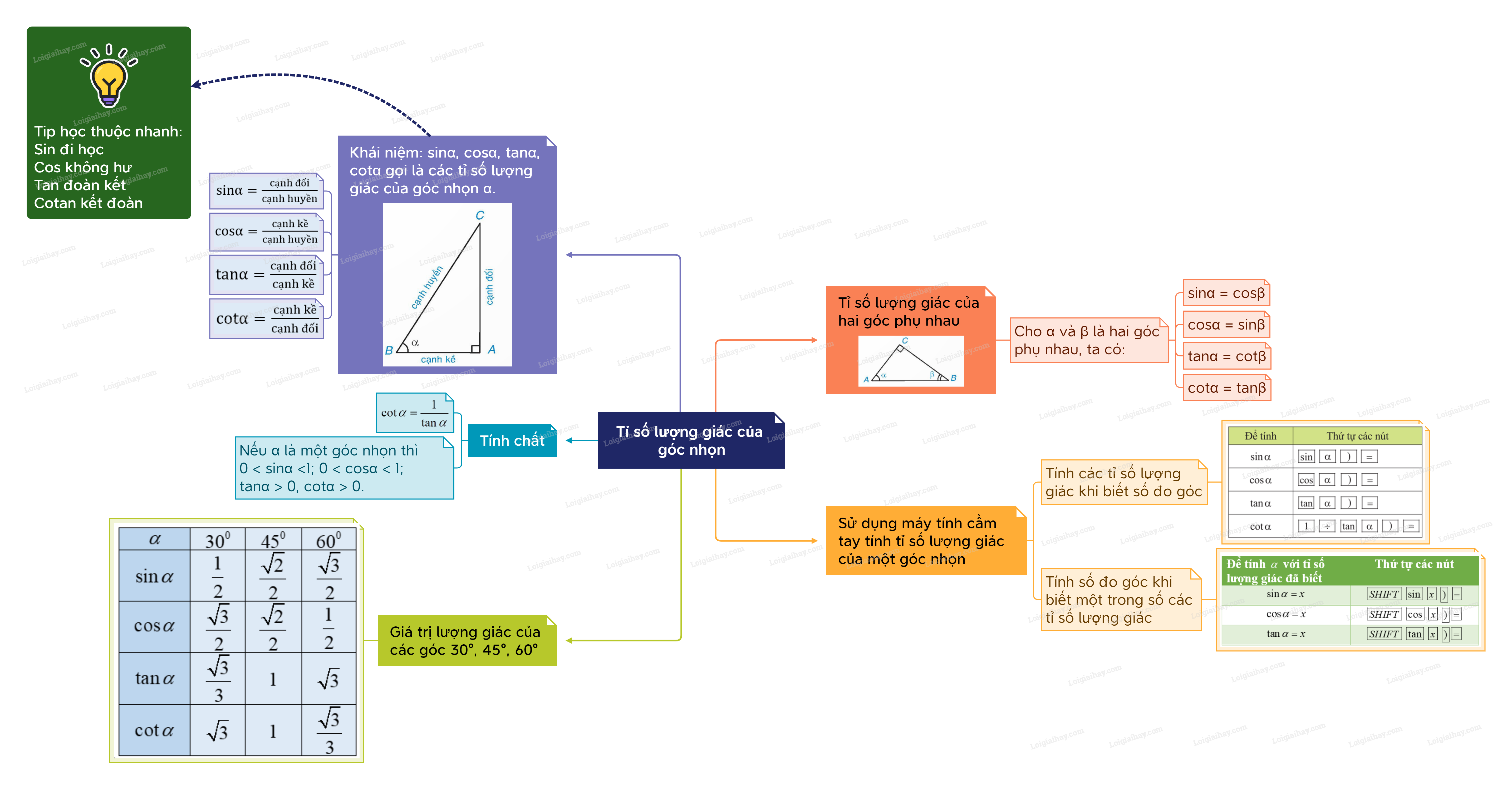
1. Khái niệm tỉ số lượng giác của một góc nhọn
Tip học thuộc nhanh:
Chú ý: Nếu \(\alpha \) là một góc nhọn thì \(0 < \sin \alpha < 1\); \(0 < \cos \alpha < 1\); \(\tan \alpha > 0\); \(\cot \alpha > 0.\) Ví dụ:
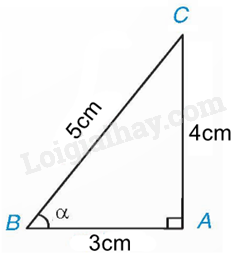
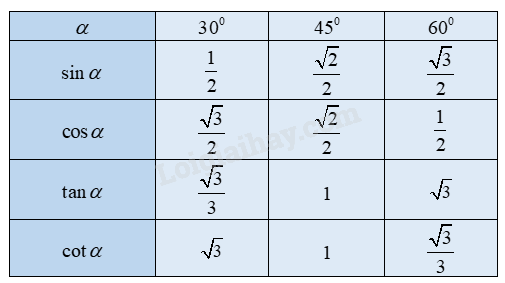
Theo định nghĩa của tỉ số lượng giác, ta có: \(\sin \alpha = \frac{{AC}}{{BC}} = \frac{4}{5}\), \(\cos \alpha = \frac{{AB}}{{BC}} = \frac{3}{5}\), \(\tan \alpha = \frac{{AC}}{{AB}} = \frac{4}{3}\), \(\cot \alpha = \frac{{AB}}{{AC}} = \frac{3}{4}\) Giá trị lượng giác của các góc \({30^0},{45^0},{60^0}\)
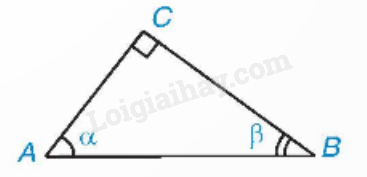
2. Tỉ số lượng giác của hai góc phụ nhau Định lí về tỉ số lượng giác của hai góc phụ nhau
Cho \(\alpha \) và \(\beta \) là hai góc phụ nhau, ta có: \(\sin \alpha = \cos \beta \), \(\cos \alpha = \sin \beta \), \(\tan \alpha = \cot \beta \), \(\cot \alpha = \tan \beta \). Ví dụ: \(\begin{array}{l}\sin {60^0} = \cos \left( {{{90}^0} - {{60}^0}} \right) = \cos {30^0};\\\cos {52^0}30' = \sin \left( {{{90}^0} - {{52}^0}30'} \right) = \sin {37^0}30';\\\tan {80^0} = \cot \left( {{{90}^0} - {{80}^0}} \right) = \cot {10^0};\\\cot {82^0} = \tan \left( {{{90}^0} - {{82}^0}} \right) = \tan {8^0}.\end{array}\) 3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn Sử dụng máy tính cầm tay để tính các tỉ số lượng giác
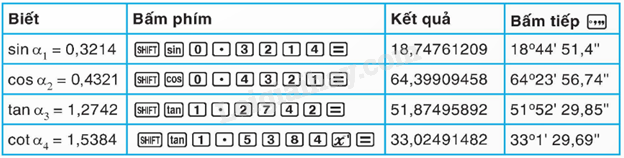
Sử dụng máy tính cầm tay để tìm được góc khi biết một trong các tỉ số lượng giác của góc đó
Một số công thức mở rộng: +) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) +) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\) +) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\) +) \(\tan \alpha .\cot \alpha = 1\) +) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\) +) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha + 1\)
|





















Danh sách bình luận