Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cánh diều1. Mẫu số liệu ghép nhóm Để chuyển mẫu số liệu không ghép nhóm thành mẫu số liệu ghép nhóm, ta có thể thực hiện như sau: − Tìm nửa khoảng [a ; b) sao cho giá trị của mỗi số liệu trong mẫu số liệu đều thuộc nửa khoảng [a ; b); Ta thường phân chia nửa khoảng [a ; b) thành các nửa khoảng có độ dài bằng nhau. Quảng cáo
1. Mẫu số liệu ghép nhóm
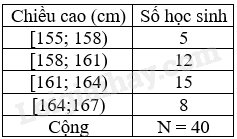
Chú ý: Khi ghép nhóm số liệu, đầu mút của các nhóm có thể không phải là giá trị của mẫu số liệu. Ví dụ: Với mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A như sau:
Số liệu có giá trị nhỏ nhất là 155, số liệu có giá trị lớn nhất là 166 , vì thế ta chọn nửa khoảng [155; 167). Vì độ dài nửa khoảng bằng 167 – 155 = 12 nên ta có thể phân chia nửa khoảng đó thành sáu nửa khoảng có độ dài bằng nhau là: [155; 158), [158; 161), [161; 164), [164;167). 2. Tần số ghép nhóm, bảng tần số ghép nhóm, biểu đồ tần số ghép nhóm Tần số ghép nhóm
Bảng tần số ghép nhóm
Chú ý: Bảng tần số ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên. Ví dụ: Ta có bảng tần số ghép nhóm cho mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A với các nhóm [155; 158), [158; 161), [161; 164), [164;167) ở dạng bảng ngang:
hoặc ở dạng bảng dọc:
Biểu đồ tần số ghép nhóm
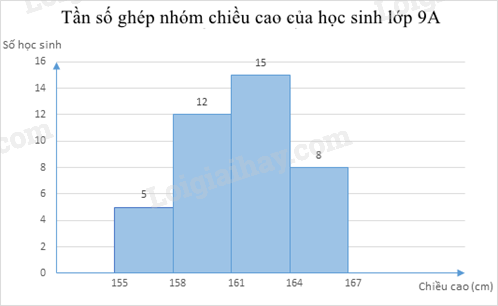
Ví dụ: Biểu đồ tần số ghép nhóm chiều cao của học sinh lớp 9A:
2. Tần số tương đối ghép nhóm, bảng tần số tương đối ghép nhóm, biểu đồ tần số tương đối ghép nhóm Tần số tương đối ghép nhóm
Bảng tần số tương đối ghép nhóm
Chú ý: Bảng tần số tương đối ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự như trên. Ví dụ: Bảng tần số ghép nhóm cho mẫu số liệu chiều cao (đơn vị là cm) của học sinh lớp 9A với các nhóm [155; 158), [158; 161), [161; 164), [164;167):
Từ bảng tần số ghép nhóm trên, ta có: Tổng số học sinh của lớp \(n = 5 + 12 + 15 + 8 = 40\). Tỉ số học sinh có chiều cao từ 150 cm đến dưới 158 cm là \(\frac{5}{{40}} = 12,5\% \); từ 158 cm đến dưới 161 cm là \(\frac{{12}}{{40}} = 30\% \); từ 161 đến dưới 164 cm là \(\frac{{15}}{{40}} = 37,5\% \); từ 164 đến dưới 167 cm là \(\frac{8}{{40}} = 20\% \). Bảng tần số tương đối ghép nhóm cho mẫu số này với các nhóm [155; 158), [158; 161), [161; 164), [164;167) là:
Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột
Biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ đoạn thẳng
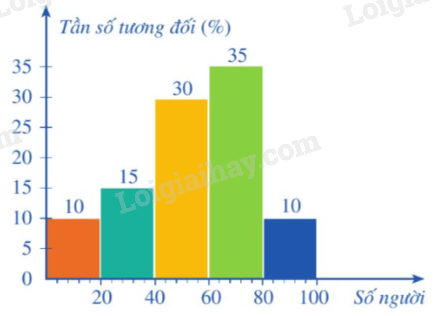
Ví dụ: Bảng tần số tương đối ghép nhóm của mẫu số liệu thống kê số lượng người đến đọc sách trong 100 ngày liên tiếp của một thư viện.
Biểu đồ tần số tương đối ghép nhóm dạng cột của bảng tần số tương đối trên là:
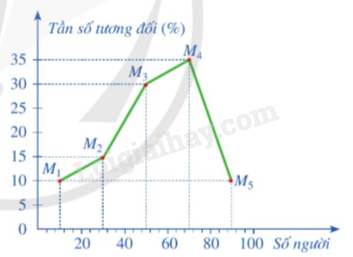
Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng của bảng tần số tương đối trên là:
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
