Lý thuyết Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn Toán 9 Kết nối tri thức1. Phương trình bậc nhất hai ẩn Khái niệm phương trình bậc nhất hai ẩn Quảng cáo
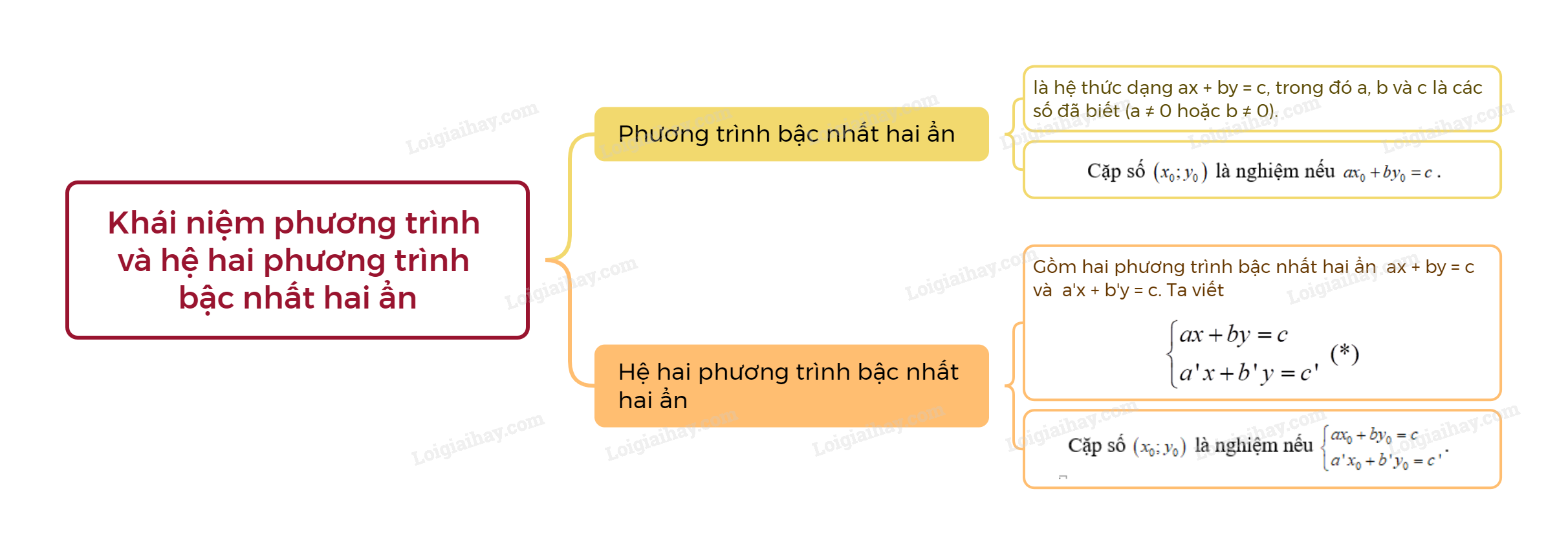
1. Phương trình bậc nhất hai ẩn Khái niệm phương trình bậc nhất hai ẩn
Ví dụ: \(2x + 3y = 4\), \(0x + 2y = 3\), \(x + 0y = 2\) là các phương trình bậc nhất hai ẩn. Nghiệm của phương trình bậc nhất hai ẩn
Ví dụ: Cặp số \(( - 1;2)\) là nghiệm của phương trình \(2x + 3y = 4\) vì \(2.\left( { - 1} \right) + 3.2 = - 2 + 6 = 4\). Cặp số \((1;2)\) không là nghiệm của phương trình \(2x + 3y = 4\) vì \(2.1 + 3.2 = 2 + 6 = 8 \ne 4\). 2. Hệ hai phương trình bậc nhất hai ẩn Khái niệm hệ hai phương trình bậc nhất hai ẩn
Ví dụ: Hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}3x = 1\\x - y = 3\end{array} \right.\), \(\left\{ \begin{array}{l}4x - y = 3\\3y = 6\end{array} \right.\) là các hệ phương trình bậc nhất hai ẩn. Nghiệm của hệ hai phương trình bậc nhất hai ẩn
Ví dụ: Cặp số (1; 2) là một nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x - y = 0\\x + y = 3\end{array} \right.\), vì: \(2x - y = 2.1 - 2 = 0\) nên (1; 2) là nghiệm của phương trình thứ nhất. \(x + y = 1 + 2 = 3\) nên (1; 2) là nghiệm của phương trình thứ hai.
|




















Danh sách bình luận