Lý thuyết Khai căn bậc hai với phép nhân và phép chia Toán 9 Kết nối tri thức1. Khai căn bậc hai và phép nhân Liên hệ giữa phép khai căn bậc hai và phép nhân Quảng cáo
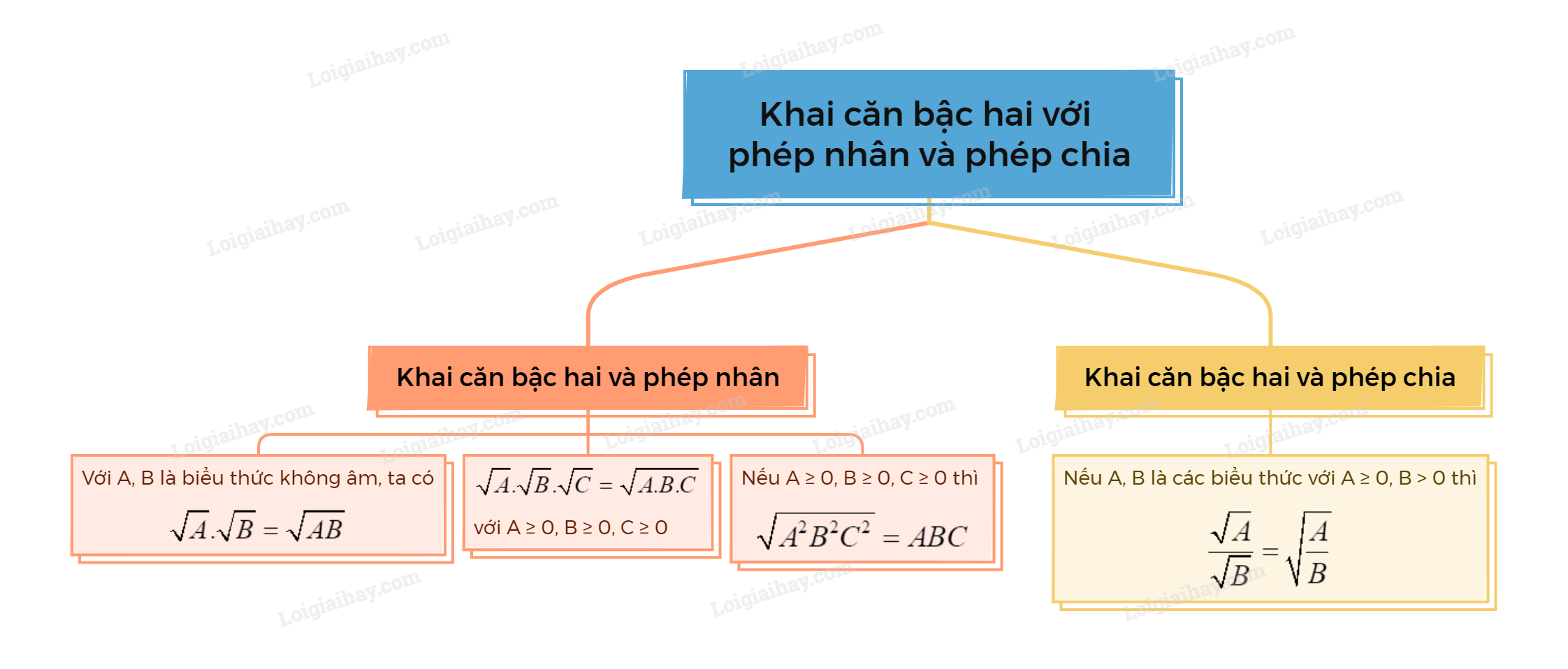
1. Khai căn bậc hai và phép nhân Liên hệ giữa phép khai căn bậc hai và phép nhân
Ví dụ: \(\sqrt {27} .\sqrt 3 = \sqrt {27.3} = \sqrt {81} = 9\) \(\sqrt 5 \left( {\sqrt {125} + \sqrt 5 } \right) = \sqrt 5 .\sqrt {125} + \sqrt 5 .\sqrt 5 = \sqrt {5.125} + \sqrt {5.5} = 25 + 5 = 30\) Chú ý: - Kết quả trên có thể mở rộng cho nhiều biểu thức không âm, chẳng hạn: \(\sqrt A .\sqrt B .\sqrt C = \sqrt {A.B.C} \) (với \(A \ge 0,B \ge 0,C \ge 0\)). Ví dụ: \(\sqrt 3 .\sqrt 5 .\sqrt {15} = \sqrt {3.5.15} = \sqrt {225} = 15\) - Nếu \(A \ge 0,B \ge 0,C \ge 0\) thì \(\sqrt {{A^2}{B^2}{C^2}} = ABC\). Ví dụ: Với \(a \ge 0,b < 0\) thì \(\sqrt {25{a^2}{b^2}} = \sqrt {{5^2}.{a^2}.{{\left( { - b} \right)}^2}} = \sqrt {{5^2}} .\sqrt {{a^2}} .\sqrt {{{\left( { - b} \right)}^2}} = 5.a.\left( { - b} \right) = - 5ab\) 2. Khai căn bậc hai và phép chia Liên hệ giữa phép khai căn bậc hai và phép chia
Ví dụ: \(\frac{{\sqrt 8 }}{{\sqrt 2 }} = \sqrt {\frac{8}{2}} = \sqrt 4 = 2\); Với \(a > 0\) thì \(\frac{{\sqrt {52{a^3}} }}{{\sqrt {13a} }} = \sqrt {\frac{{52{a^3}}}{{13a}}} = \sqrt {4{a^2}} = \sqrt {{{\left( {2a} \right)}^2}} = 2a\).
|




















Danh sách bình luận