Lý thuyết Hàm số y = ax² (a ≠ 0) Toán 9 Kết nối tri thức1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\). Quảng cáo
1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\). 2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
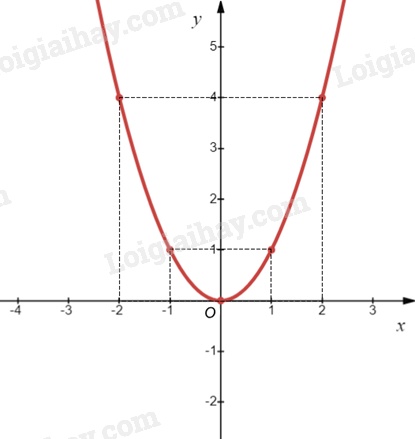
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\). Lập bảng một số giá trị tương ứng giữa x và y:
Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:
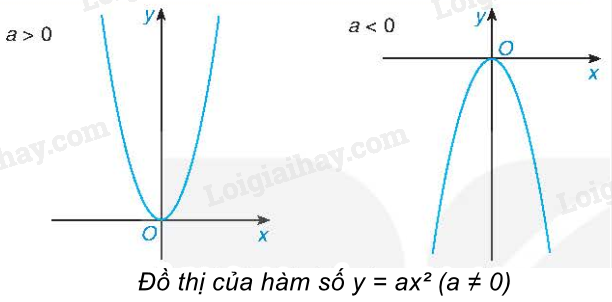
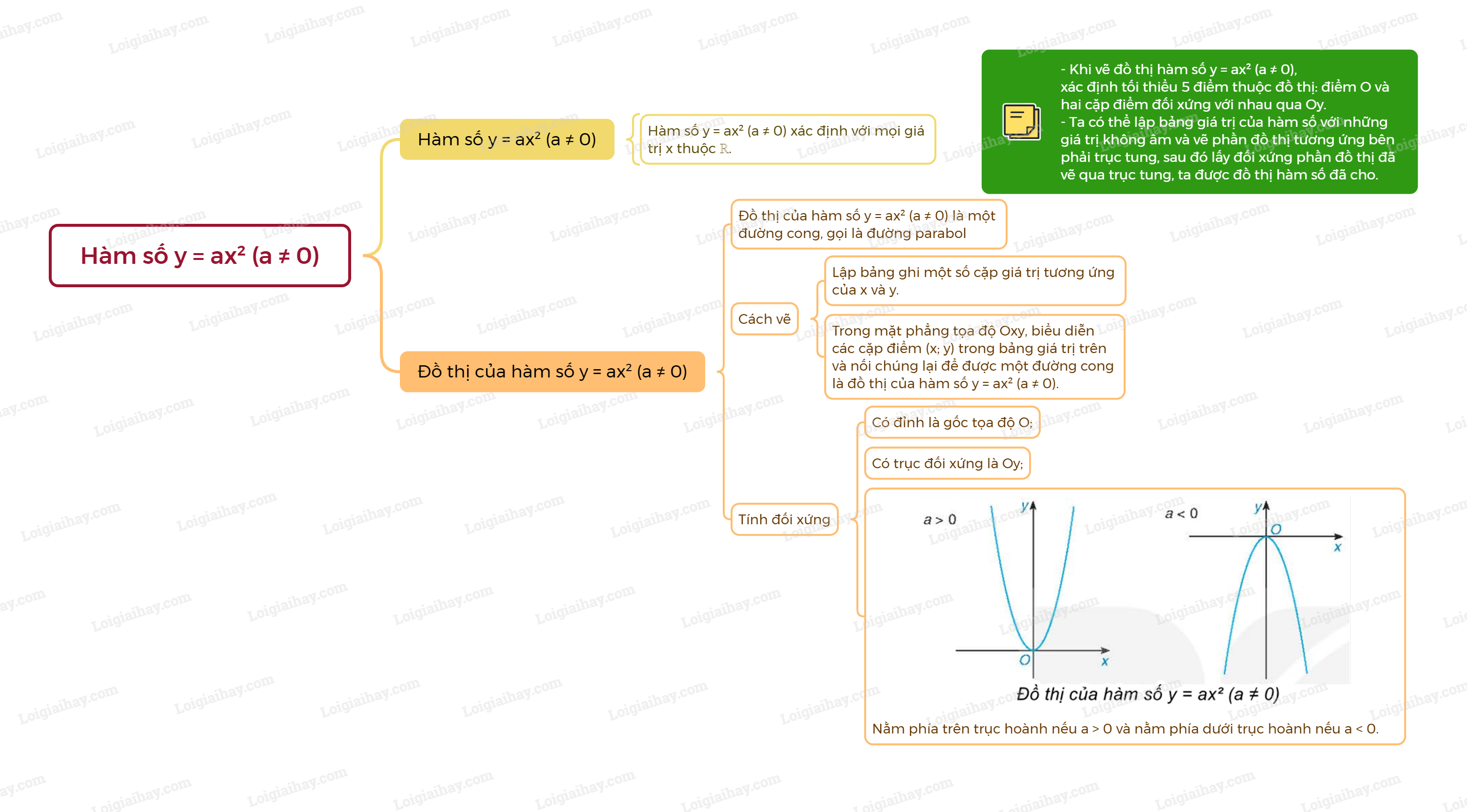
Tính đối xứng của đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)
Nhận xét: - Khi vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta cần xác định tối thiểu 5 điểm thuộc đồ thị là gốc tọa độ O và hai cặp điểm đối xứng với nhau qua trục tung Oy. - Do đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) nhận trục tung Oy là trục đối xứng nên ta có thể lập bảng giá trị của hàm số này với những giá trị x không âm và vẽ phần đồ thị tương ứng ở bên phải trục tung, sau đó lấy đối xứng phần đồ thị đã vẽ qua trục tung ta sẽ được đồ thị của hàm số đã cho.
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
