Lý thuyết Căn bậc hai và căn bậc ba của số thực Toán 9 Cánh diều

1. Căn bậc hai của số thực không âm

Chú ý:

- Khi \(a > 0\), số a có đúng hai căn bậc hai là hai số đối nhau: số dương kí hiệu là \(\sqrt a \); số âm kí hiệu là \( - \sqrt a \). Ta gọi \(\sqrt a \) là căn bậc hai số học của a.

- Căn bậc hai của số 0 bằng 0.

- Số âm không có căn bậc hai.

Ví dụ:

· \(\sqrt {81}  = 9\) nên 81 có hai căn bậc hai là 9 và -9.

· Căn bậc hai số học của 121 là \(\sqrt {121}  = 11\).

Nhận xét: Với hai số a, b không âm, ta có:

- Nếu \(a < b\) thì \(\sqrt a  < \sqrt b \);

- Nếu \(\sqrt a  < \sqrt b \) thì \(a < b\).

2. Căn bậc ba

Khái niệm căn bậc ba của một số thực

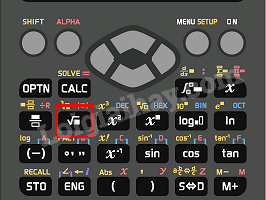
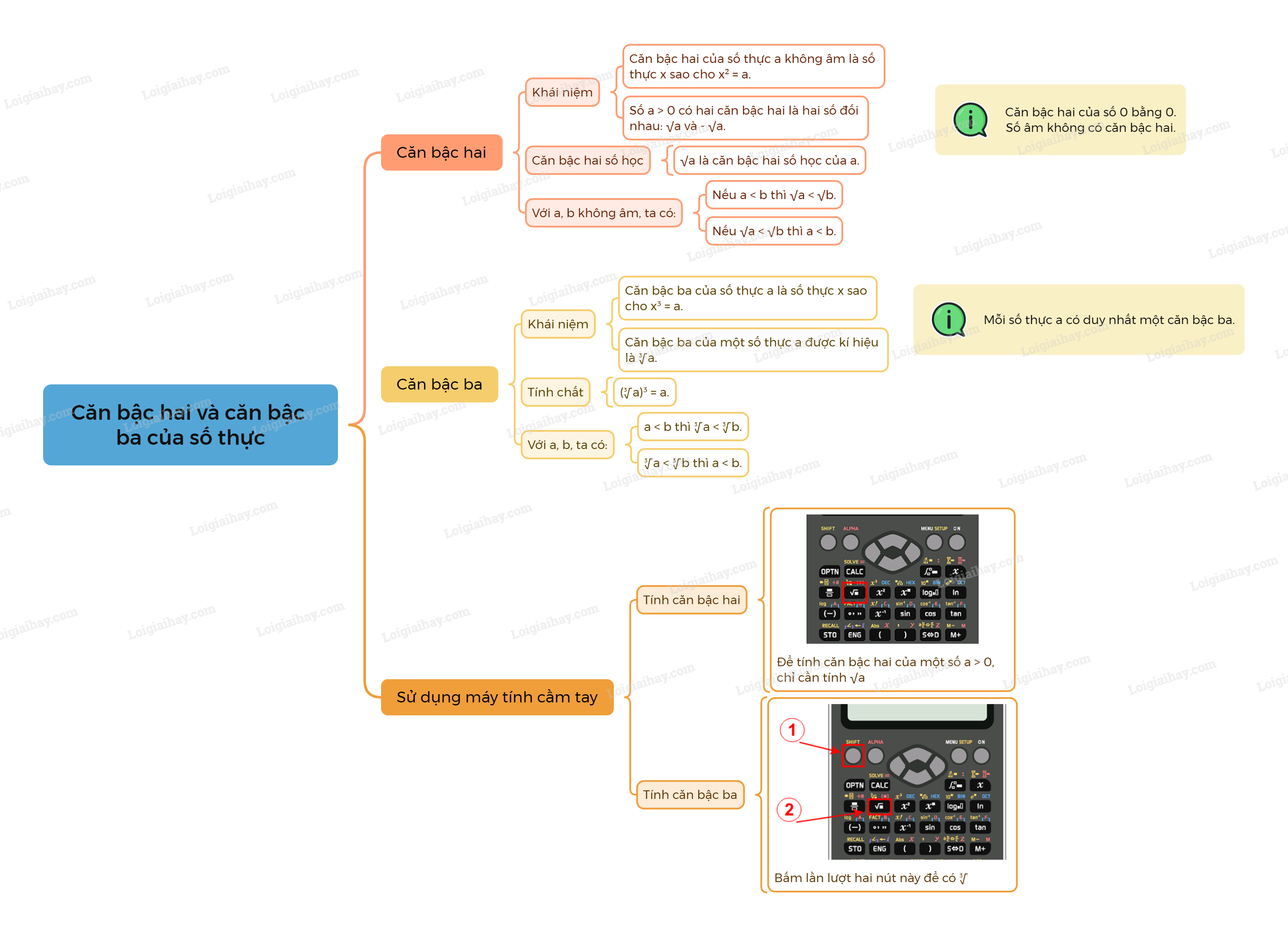
Chú ý: Mỗi số thực a đều có duy nhất một căn bậc ba.

Nhận xét: \({\left( {\sqrt[3]{a}} \right)^3} = a\).

Với hai số a, b, ta có:

- Nếu \(a < b\) thì \(\sqrt[3]{a} < \sqrt[3]{b}\).

- Nếu \(\sqrt[3]{a} < \sqrt[3]{b}\) thì \(a < b\).

Ví dụ:

\(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\);

\(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} =  - 3\).

3. Sử dụng máy tính cầm tay để tìm căn bậc hai, căn bậc ba của một số hữu tỉ

Tính căn bậc hai của một số bằng máy tính cầm tay

Tính căn bậc ba của một số bằng máy tính cầm tay

Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

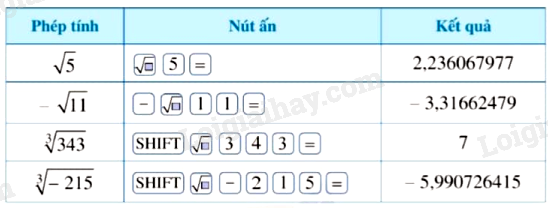
Ví dụ: