Lý thuyết Căn bậc ba và căn thức bậc ba Toán 9 Kết nối tri thức1. Căn bậc ba Khái niệm căn bậc ba của một số thực Quảng cáo
1. Căn bậc ba Khái niệm căn bậc ba của một số thực
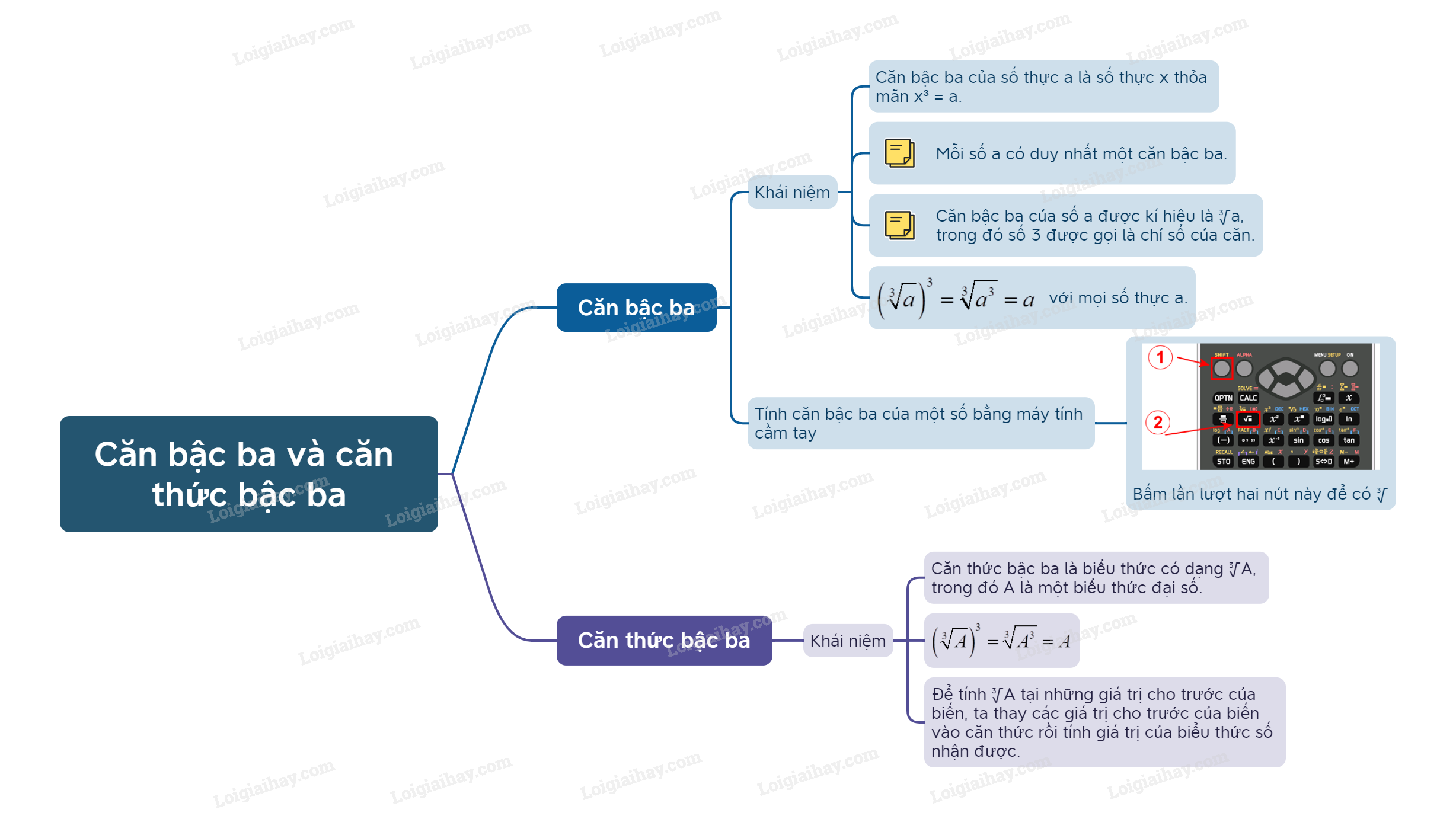
Chú ý: - Mỗi số a đều có duy nhất một căn bậc ba. - Căn bậc ba của số a được kí hiệu là \(\sqrt[3]{a}\), trong đó số 3 được gọi là chỉ số của căn. Nhận xét: Từ định nghĩa căn bậc ba, ta có \({\left( {\sqrt[3]{a}} \right)^3} = \sqrt[3]{{{a^3}}} = a\) với mọi số thực a. Ví dụ: \(\sqrt[3]{{64}} = \sqrt[3]{{{4^3}}} = 4\); \(\sqrt[3]{{ - 27}} = \sqrt[3]{{{{\left( { - 3} \right)}^3}}} = - 3\). Tính căn bậc ba của một số bằng máy tính cầm tay Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
