Lý thuyết Các số đặc trưng đo xu thế trung tâm

1. SỐ TRUNG BÌNH VÀ TRUNG VỊ

a. Số trung bình

Cho mẫu số liệu \({x_1},{x_2},{x_3},...,{x_n}\)

+) Số trung bình (hay TB cộng) của mẫu số liệu kí hiệu là \(\overline x \), được tính bằng công thức: \(\overline x  = \frac{{{x_1} + {x_2} + {x_3} + ... + {x_n}}}{n}\)

+) Mẫu số liệu cho dưới dạng bảng tần số thì:

\(\overline x  = \frac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3} + ... + {m_k}{x_k}}}{n}\)

Với \({m_i}\) là tần số của giá trị \({x_i}\) và \(n = {m_1} + {m_2} + ... + {m_k}\)

+) Ý nghĩa: Số trung bình là giá trị trung bình cộng, cho biết vị trí trung tâm của mẫu số liệu và có thể dùng để đại diện cho mẫu số liệu

b. Trung vị

+) Trong trường hợp mẫu số liệu có giá trị bất thường (rất lớn hoặc rất bé so với đa số các giá trị khác), ta dùng trung vị để đo xu thế trung tâm.

Ví dụ: mẫu số liệu: 1      3       2        3         4         20

 Tìm trung vị:

Bước 1: Sắp xếp các giá trị theo thứ tự không giảm \({X_1},{X_2},..,{X_n}\)

Bước 2: Cỡ mẫu = n.

  + Nếu n lẻ (\(n = 2k - 1\)) thì trung vị là \({X_k}\)

  + Nếu n chẵn (\(n = 2k\)) thì trung vị bằng \(\frac{1}{2}({X_k} + {X_{k + 1}})\)

+) Ý nghĩa: Trung vị là giá trị ở vị trí chính giữa của mẫu số liệu đã sắp xếp theo thứ tự không giảm. Trung vị không bị ảnh hưởng bởi giá trị bất thường như số trung bình.

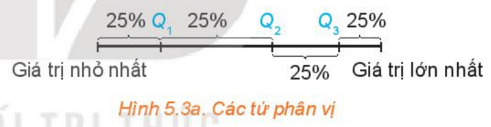
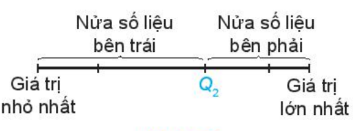
2. TỨ PHÂN VỊ

Tứ phân vị gồm 3 giá trị \({Q_1},{Q_2},{Q_3}\), nó chia mẫu số liệu đã sắp xếp

theo thứ tự từ nhỏ đến lớn thành 4 phần, mỗi phần đều chứa 25% giá trị.

+) Các bước tìm tứ phân vị:

Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm.

Bước 2: Tìm trung vị, chính là \({Q_2}\)

Bước 3: \({Q_1}\) là trung vị của nửa số liệu bên trái \({Q_2}\)(không bao gồm \({Q_2}\) nếu n lẻ).

Bước 4: \({Q_3}\)là trung vị của nửa số liệu bên phải \({Q_2}\)(không bao gồm \({Q_2}\) nếu n lẻ).

Chú ý:

\({Q_1}\) còn được gọi là tứ phân vị thứ nhất hoặc tứ phân vị dưới.

 \({Q_3}\) còn được gọi là tứ phân vị thứ ba hoặc tứ phân vị trên.

3. MỐT

+) Mốt của mẫu số liệu là giá trị xuất hiện với tần số lớn nhất

+) Ý nghĩa: Dùng mốt để đo xu thế trung tâm của mẫu số liệu khi mẫu có nhiều giá trị trùng nhau.

+) Nhận xét

  - Mốt có thể không là duy nhất. Một mẫu có thể có nhiều mốt

  - Khi các giá trị trong mẫu xuất hiện với tần số như nhau thì mẫu số liệu đó không có mốt.