Giải mục 4 trang 41, 42 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ4

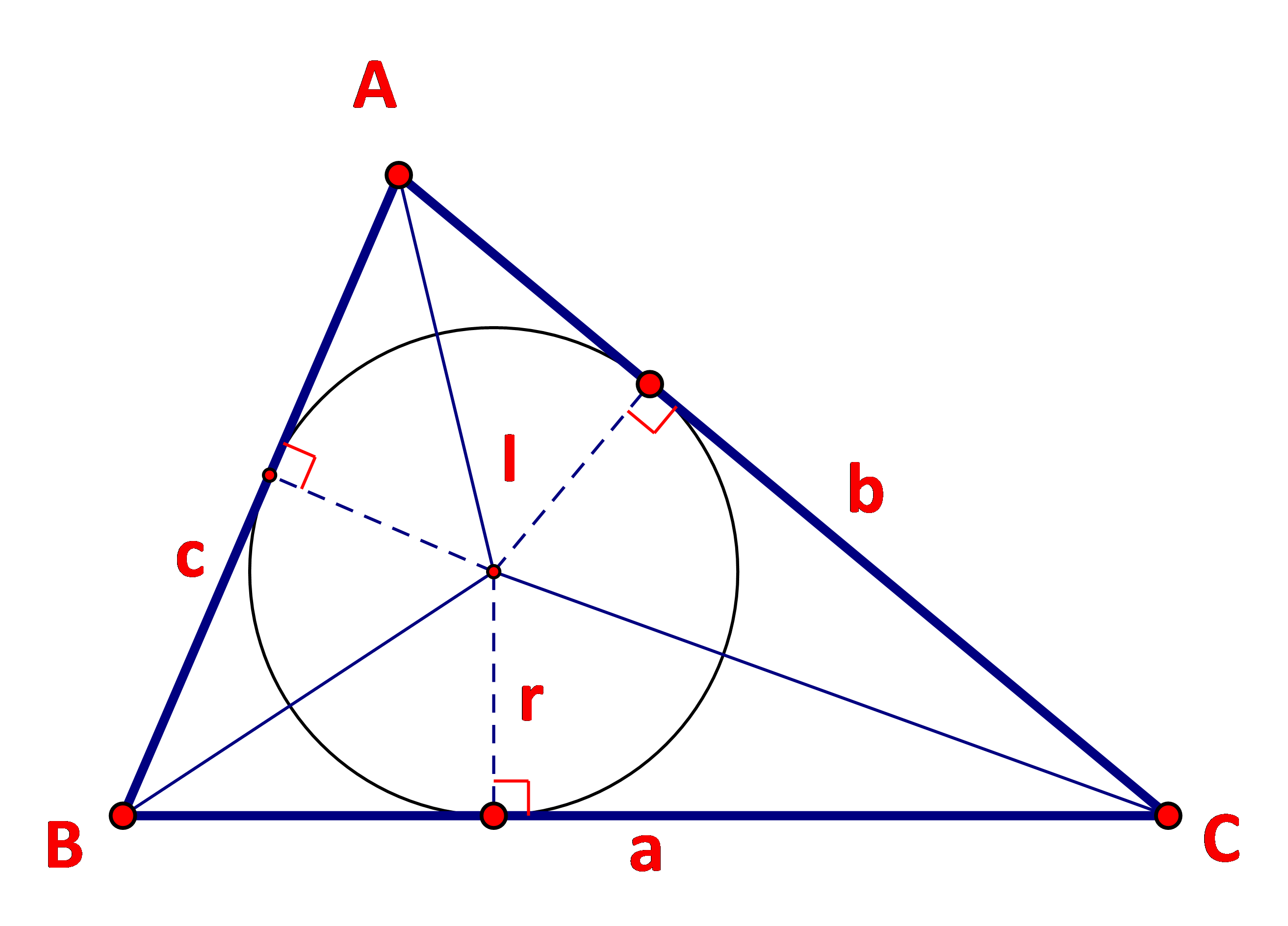
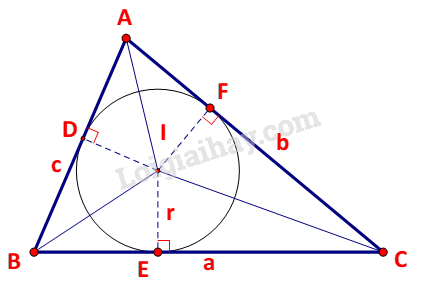
Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác.

a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích các tam giác IBC, ICA, IAB.

b) Tính diện tích tam giác ABC theo r,a,b,c.

Phương pháp giải:

a) Tính diện tích tam giác ABC theo diện tích các tam giác IBC, ICA, IAB.

b) Diện tích tam giác IBC: \({S_{IBC}} = \frac{1}{2}r.a\).

Lời giải chi tiết:

a) Diện tích tam giác ABC là: \[S = {S_{IAB}} + {S_{IBC}} + {S_{IAC}}\]

b)

Kí hiệu: D,E, F lần lượt là hình chiếu của I trên AB, BC, AC.

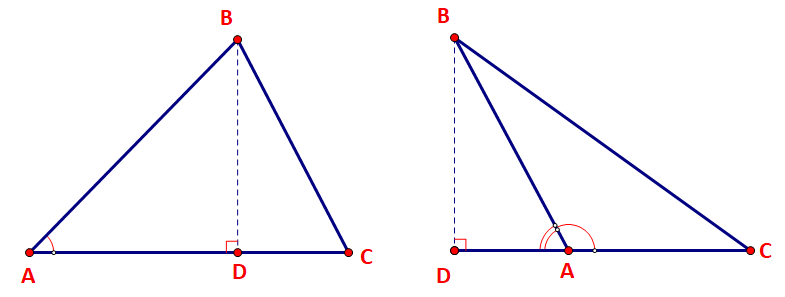
Ta có:

\(\begin{array}{l}{S_{IAB}} = \frac{1}{2}.ID.AB = \frac{1}{2}r.c\\{S_{IBC}} = \frac{1}{2}IE.BC = \frac{1}{2}r.a\\{S_{IAC}} = \frac{1}{2}IF.AC = \frac{1}{2}r.b\end{array}\)

\( \Rightarrow S = \frac{1}{2}r.c + \frac{1}{2}r.a + \frac{1}{2}r.b = \frac{1}{2}r.\left( {a + b + c} \right)\)

Vậy diện tích tam giác ABC tính theo r, a, b, c là \(S = \frac{1}{2}r.\left( {a + b + c} \right)\).

HĐ5

Cho tam giác ABC với đường cao BD.

a) Biểu thị BD theo AB và sinA.

b) Viết công thức tính diện tích S của tam giác ABC theo b,c, sin A.

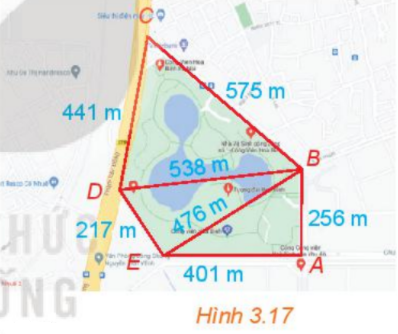
Phương pháp giải:

a) Biểu thị BD dựa vào sin A (hoặc \(\sin \left( {{{180}^o} - {\rm{ }}A} \right)\)) trong tam giác vuông ABD.

b)

+) Tính \({S_{ABC}} = \frac{1}{2}BD.AC\)

+) Thay BD ở ý a) để suy ra công thức tính S theo b,c và sin A.

Lời giải chi tiết:

a) Xét tam giác vuông ABD vuông tại D ta có:

TH1: góc A nhọn

\(\sin A = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)

TH2: góc A tù

\(\sin A = \sin ({180^o} - A) = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)

Vậy \(BD = AB.\sin A\)

b) Ta có diện tích S của tam giác ABC là: \(S = \frac{1}{2}BD.AC\)

Mà \(BD = AB.\sin A = c.\sin A\); BC = a. Thế vào (*) ta được:

\(S = \frac{1}{2}c.\sin A.b\) hay \(S = \frac{1}{2}bc.\sin A.\)

Vậy diện tích S của tam giác ABC theo b, c, sin A là \(S = \frac{1}{2}bc.\sin A.\)

Luyện tập 4

Tính diện tích tam giác ABC có \(b = 2,\;\widehat B = {30^o},\;\widehat C = {45^o}\).

Phương pháp giải:

\(S = \frac{1}{2}bc.\sin A.\)

Bước 1: Tính c bằng cách áp dụng định lí sin.

Bước 2: Tính góc \(\;\widehat A\), tính \(S = \frac{1}{2}bc.\sin A.\)

Lời giải chi tiết:

Áp dụng định lí sin cho tam giác ABC ta có:

\(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)

\( \Rightarrow c = \sin C.\frac{b}{{\sin B}} = \sin {45^o}.\frac{2}{{\sin {{30}^o}}} = 2\sqrt 2 \)

Lại có: \(\;\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {30^o} - {45^o} = {105^o}\)

Do đó diện tích tích S của tam giác ABC là:

\(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.2.2\sqrt 2 .\sin {105^o} = 1 + \sqrt 3 .\)

Vậy diện tích tam giác ABC là \(1 + \sqrt 3 \).

Thảo luận

Ta đã biết tính cos A theo độ dài các cạnh của tam giác ABC. Liệu sin A và diện tích S có tính theo độ dài các cạnh của tam giác ABC hay không?

Phương pháp giải:

Nhắc lại:

+) công thức tính diện tích tam giác ABC: \(S = \frac{1}{2}bc.\sin A.\)

+) \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)

Bước 1: Tính sin A theo cos A. Lưu ý: \(\sin A > 0\)

Bước 2: Thay sin A vào \(S = \frac{1}{2}bc.\sin A.\) Rút gọn biểu thức rồi kết luận.

Lời giải chi tiết:

Từ định lí cosin trong tam giác ABC, ta suy ra: \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)

Mà \({\sin ^2}A + {\cos ^2}A = 1\)

\( \Rightarrow \sin A =  \pm \sqrt {1 - {{\cos }^2}A} \)

Do \({0^o} < \widehat A < {180^o}\) nên \(\sin A > 0\) hay \(\sin A = \sqrt {1 - {{\cos }^2}A} \)

Ta có:

\(\begin{array}{l}\sin A = \sqrt {1 - {{\left( {\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}} \right)}^2}}  = \sqrt {1 - \frac{{{{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}} \\ = \sqrt {\frac{{4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}}}{{4{b^2}{c^2}}}}  = \frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}}\end{array}\)

Thế vào công thức tính diện tích tam giác ABC ta được:

\(S = \frac{1}{2}bc.\frac{{\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} }}{{2bc}} = \frac{1}{4}.\sqrt {4{b^2}{c^2} - {{\left( {{b^2} + {c^2} - {a^2}} \right)}^2}} \)

Chú ý:

Nếu tiếp tục biến đổi công thức diện tích ta được

\(\begin{array}{l}S = \frac{1}{4}.\sqrt {\left( {2bc + {b^2} + {c^2} - {a^2}} \right)\left( {2bc - {b^2} - {c^2} + {a^2}} \right)} \\ = \frac{1}{4}.\sqrt {\left[ {{{\left( {b + c} \right)}^2} - {a^2}} \right]\left[ {{a^2} - {{\left( {b - c} \right)}^2}} \right]} \\ = \frac{1}{4}.\sqrt {\left( {b + c - a} \right)\left( {b + c + a} \right)\left( {a - b + c} \right)\left( {a + b - c} \right)} \end{array}\)

Đến đây, đặt \(p = \frac{{a + b + c}}{2}\), là nửa chu vi tam giác ABC, ta suy ra:

\(\left\{ \begin{array}{l}b + c + a = 2p\\b + c - a = b + c + a - 2a = 2\left( {p - a} \right)\\a - b + c = b + c + a - 2b = 2\left( {p - b} \right)\\a + b - c = b + c + a - 2c = 2\left( {p - c} \right)\end{array} \right.\)

\(\begin{array}{l} \Rightarrow S = \frac{1}{4}\sqrt {2\left( {p - a} \right).2p.2\left( {p - b} \right).2\left( {p - c} \right)} \\ \Leftrightarrow S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \end{array}\)

(công thức Heron)

Vận dụng 3

Công viên Hòa Bình (Hà Nội) có dạng hình ngũ giác ABCDE như hình 3.17. Dùng chế dộ tình khoảng cách giữa hai điểm của Google Maps, một người xác định được các khoảng cách như trong hình vẽ. Theo số liệu đó, em hãy tính diện tích của công viên hòa bình.

Phương pháp giải:

Bước 1: Tính diện tích các tam giác CBD, DBE, EBA bằng công thức Herong:

\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)

Bước 2: Tính diện tích ngũ giác ABCDE, bằng tổng diện tích các tam giác CBD, DBE, EBA.

Lời giải chi tiết:

Xét tam giác CDB, ta có: CD = 441, CB = 575 và DB = 538 (đơn vị: m)

Và nửa chu vi là: \(\frac{{441 + 575 + 538}}{2} = 777(m)\)

Do đó: \({S_{CDB}} = \sqrt {777.\left( {777 - 441} \right).\left( {777 - 575} \right).\left( {777 - 538} \right)}  \approx 112267,7\left( {{m^2}} \right)\)

Xét tam giác DBE, ta có: DE = 217, EB = 476 và DB = 538 (đơn vị: m)

Và nửa chu vi là: \(\frac{{217 + 476 + 538}}{2} = 615,5(m)\)

Do đó: \({S_{DBE}} = \sqrt {615,5.\left( {615,5 - 217} \right).\left( {615,5 - 476} \right).\left( {615,5 - 538} \right)}  \approx 51495,13\left( {{m^2}} \right)\)

Xét tam giác ABE, ta có: AE = 401, EB = 476 và BA =256 (đơn vị: m)

Và nửa chu vi là: \(\frac{{401 + 476 + 256}}{2} = 566,5(m)\)

Do đó: \({S_{ABE}} = \sqrt {566,5.\left( {566,5 - 401} \right).\left( {566,5 - 476} \right).\left( {566,5 - 256} \right)}  \approx 51327,97\left( {{m^2}} \right)\)

Vậy diện tích S của ngũ giác ABCDE là: \(S = {S_{CDB}} + {S_{DBE}} + {S_{ABE}} \approx 112267,7 + 51495,13 + 51327,97 = 215090,8\left( {{m^2}} \right)\)

Chú ý

+) Để tính diện tích ngũ giác ABCDE thông qua các tam giác nhỏ, ta cần chọn các tam giác thỏa mãn: “phần trong của chúng không đè lên nhau” và “ghép lại vừa khít tạo thành ngũ giác ABCDE”

+) Ưu tiên tính thông qua các tam giác đã biết đủ các cạnh.