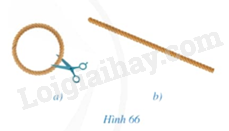
Giải mục 1 trang 118, 119 SGK Toán 9 tập 1 - Cánh diều

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 118 SGK Toán 9 Cánh diều

Lấy một vòng tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b. Đo chiều dài sợi dây đó. 

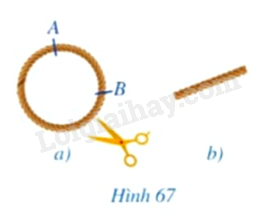
Phương pháp giải:

Dùng thước kẻ để đo độ dài.

Lời giải chi tiết:

HS tự thực hiện theo yêu cầu.

LT1

Trả lời câu hỏi Luyện tập 1 trang 118 SGK Toán 9 Cánh diều

Tính chu vi của đường tròn bán kính 5 cm (theo đơn vị centimét và làm tròn kết quả đến hàng phần mười).

Phương pháp giải:

Dựa vào công thức tính chu vi đường tròn: \(C = 2\pi R\) để tính.

Lời giải chi tiết:

Chu vi của đường tròn là:

\(C = 2\pi R = 2\pi .5 = 10\pi  \approx 31,4\left( {cm} \right)\).

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 119 SGK Toán 9 Cánh diều

a) Đánh dấu hai điểm \(A,B\) trên một vòng dây không dãn có dạng đường tròn (Hình 67a), cắt cung \(AB\) của vòng dây và kéo thẳng cung đó để nhận được sợi dây như ở Hình 67b. Đo chiều dài sợi dây đó.

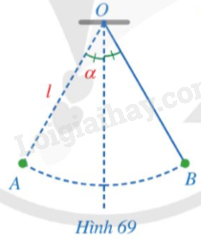
b) Ta coi mỗi đường tròn bán kính \(R\) là một cung tròn có số đo \(360^\circ \). Chia đường tròn đó thành 360 phần bằng nhau, mỗi phần là cung tròn có số đo bằng \(1^\circ \); chu vi của đường tròn khi đó cũng được chia thành \(360\) phần bằng nhau. Tính theo \(R\):

+ Độ dài cung tròn có số đo \(1^\circ \);

+ Độ dài cung tròn có số đo \(n^\circ \).

Phương pháp giải:

Dựa vào kiến thức vừa học để tính.

Lời giải chi tiết:

a) Chiều dài sợi dây \(AB\) là: 5cm.

b) Độ dài cung tròn có số đo \(1^\circ \) là:

\(l = \frac{{2\pi R}}{{360}} = \frac{{\pi R}}{{180}}\).

Độ dài cung tròn có số đo \(n^\circ \) là:

\(l = \frac{{2\pi Rn}}{{360}} = \frac{{\pi Rn}}{{180}}\).

LT2

Trả lời câu hỏi Luyện tập 2 trang 119 SGK Toán 9 Cánh diều

Một con lắc di chuyển từ vị trí \(A\) đến vị trí \(B\) (Hình 69). Tính độ dài quãng đường \(AB\) mà con lắc đó di chuyển, biết rằng sợi dây \(OA\) có độ dài bằng \(l\) và tia \(OA\) tạo với phương thẳng đứng góc \(\alpha \).

Phương pháp giải:

Dựa vào công thức tính độ dài cung tròn \(l = \frac{{\pi Rn}}{{180}}\) để tính.

Lời giải chi tiết:

Độ dài quãng đường \(AB\) mà con lắc đó di chuyển là:

\(AB = \frac{{\pi .l.2\alpha }}{{180}} = \frac{{\pi l\alpha }}{{90}}.\)