Giải mục 1 trang 11, 12 SGK Toán 10 tập 2 - Kết nối tri thức

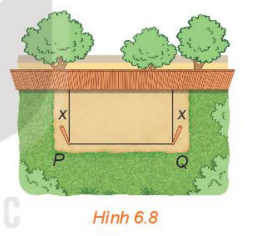
HĐ1

Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét \((0 < x < 10)\) là khoảng cách từ điểm cắm cọc đến bờ tường (H.6.8). Hãy tính theo x:

a) Độ dài cạnh PQ của mảnh đất.

b) Diện tích S(x) của mảnh đất được rào chắn.

Lời giải chi tiết:

a) Theo bài ra ta có:

\(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\) (m).

b) Diện tích của mảnh đất được rào chắn là:

\(x.PQ = x.(20 - 2x) =  - 2{x^2} + 20x\) \(({m^2})\).

CH

Hàm số nào dưới đây là hàm số bậc hai?

A. \(y = {x^4} + 3{x^2} + 2\);

B.\(y = \frac{1}{{{x^2}}}\);

C.\(y =  - 3{x^2} + 1\);

D.\(y = 3{\left( {\frac{1}{x}} \right)^2} + 3.\frac{1}{x} - 1\).

Phương pháp giải:

Hàm số bậc hai là hàm số có dạng: \(y = a{x^2} + bx + c\) \((a \ne 0)\).

Lời giải chi tiết:

Hàm số \(y =  - 3{x^2} + 1\) là hàm số bậc hai.

LT1

Cho hàm số \(y = (x - 1)(2 - 3x)\).

a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.

b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho.

Phương pháp giải:

Hàm số có dạng \(a{x^2} + bx + c(a \ne 0)\) là hàm số bậc hai.

Lời giải chi tiết:

a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x \)

\(=  - 3{x^2} + 5x - 2\).

Do đó hàm \(y=(x-1)(2-3x)\) là hàm số bậc hai với \(a =  - 3\); \(b = 5\); \(c =  - 2\).

b) Thay các giá trị của x vào \(y=(x-1)(2-3x)\) ta có:

VD1

Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: \(h = 19,6 - 4,9{t^2}\); \(h\), \(t \ge 0\).

a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?

b) Tìm tập xác định và tập giá trị của hàm số h.

Lời giải chi tiết:

a) Để viên bi chạm đất thì \(h = 0 \Leftrightarrow 19,6 - 4,9{t^2} = 0\)

\(\Leftrightarrow 4,9{t^2} = 19,6 \Leftrightarrow {t^2} = 4\).

Do \(t \ge 0\) nên t = 2 (s).

Vậy sau 2 giây thì viên bi chạm đất.

b) Theo bài ra ta có: \(t \ge 0\) nên tập xác định của hàm số h là \(D = \left[ {0; + \infty } \right)\).

Mặt khác: \(4,9{t^2} \ge 0 \Rightarrow 19,6 - 4,9{t^2} \le 19,6\).

\( \Rightarrow 0 \le h \le 19,6\). Do đó tập giá trị của hàm số h là \(\left[ {0;19,6} \right]\).