Giải mục 1 trang 106, 107 SGK Toán 9 tập 1 - Cánh diềuCho đường thẳng (a) là tiếp tuyến của đường tròn (left( {O;R} right)). Gọi (H) là hình chiếu của tâm (O) trên đường thẳng (a) (Hình 33). a) So sánh khoảng cách (OH) từ tâm (O) đến đường thẳng (a) và bán kính (R). b) Điểm (H) có thuộc đường tròn (left( {O;R} right)) hay không? c) Điểm (H) có phải là tiếp điểm của đường thẳng (a) và đường tròn (left( {O;R} right)) hay không? d) Đường thẳng (a) có vuông góc với bán kính đi qua tiếp điểm hay không? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
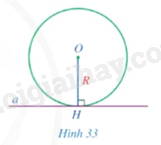
HĐ1 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 1 trang 106 SGK Toán 9 Cánh diều Cho đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\). Gọi \(H\) là hình chiếu của tâm \(O\) trên đường thẳng \(a\) (Hình 33).
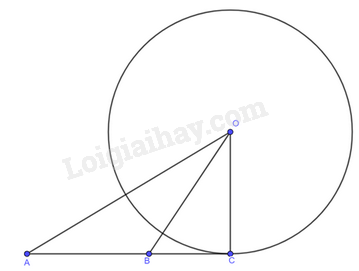
a) So sánh khoảng cách \(OH\) từ tâm \(O\) đến đường thẳng \(a\) và bán kính \(R\). b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không? c) Điểm \(H\) có phải là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) hay không? d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm hay không? Phương pháp giải: Dựa vào hình ảnh trực quan để trả lời câu hỏi. Lời giải chi tiết: a) \(OH = R\). b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\). c) Điểm \(H\) là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\). d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm. LT1 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 1 trang 107 SGK Toán 9 Cánh diều Cho ba điểm \(A,B,C\) thẳng hàng, trong đó \(B\) nằm giữa \(A\) và \(C\). Đường tròn \(\left( O \right)\) tiếp xúc với đường thẳng \(AB\) tại điểm \(C\). Chứng minh: \(A{O^2} + B{C^2} = B{O^2} + A{C^2}\). Phương pháp giải: Dựa vào kiến thức vừa học để chứng minh. Lời giải chi tiết:
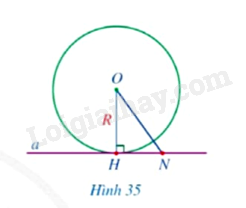
Vì đường thẳng \(AB\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(C\) nên \(OC \bot AB\). Suy ra tam giác \(OBC\) vuông tại \(C\), tam giác \(OAC\) vuông tại C. Áp dụng định lý Pythagore vào tam giác \(OAC\) vuông tại \(C\), ta có: \(O{A^2} = O{C^2} + A{C^2} \Rightarrow O{C^2} = O{A^2} - A{C^2}\,\,\left( 1 \right)\). Áp dụng định lý Pythagore vào tam giác \(OBC\) vuông tại \(C\), ta có: \(O{B^2} = O{C^2} + B{C^2} \Rightarrow O{C^2} = O{B^2} - B{C^2}\,\,\,\left( 2 \right)\). Từ (1) và (2) suy ra \(O{A^2} - A{C^2} = O{B^2} - B{C^2} \Rightarrow O{A^2} + B{C^2} = O{B^2} + A{C^2}\). HĐ2 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 2 trang 107 SGK Toán 9 Cánh diều Cho đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) thỏa mãn đường thẳng \(a\) đi qua điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) và \(a \bot OH\).
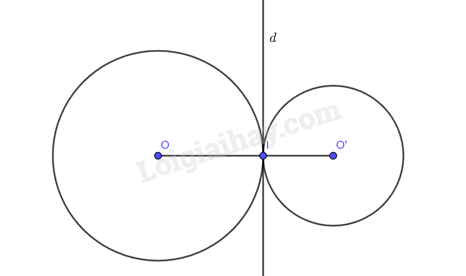
a) So sánh khoảng cách từ điểm \(O\) đến đường thẳng \(a\) và bán kính \(R\). b) Giả sử \(N\) là điểm thuộc đường thẳng \(a\) và \(N\) khác \(H\). So sánh \(ON\) và \(R\). Điểm \(N\) có thuộc đường tròn \(\left( {O;R} \right)\) hay không? c) Đường thẳng \(a\) có phải là tiếp tuyến của đường tròn \(\left( {O;R} \right)\) hay không? Phương pháp giải: Dựa vào hình ảnh trực quan và các kiến thức đã học để trả lời câu hỏi. Lời giải chi tiết: a) Khoảng cách từ điểm \(O\) đến đường thẳng \(a\) là đoạn \(OH\). Do điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) nên \(OH = R\). Vậy khoảng cách từ điểm \(O\) đến đường thẳng \(a\) bằng bán kính \(R\). b) Xét tam giác \(OHN\) vuông tại \(H\) có: \(ON\) là cạnh huyền, \(OH\) là cạnh góc vuông. Suy ra \(ON > OH\), lại có \(OH = R\). Vậy \(ON > R\). Điểm \(N\) không thuộc đường tròn \(\left( {O;R} \right)\). c) Đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\). LT2 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 2 trang 107 SGK Toán 9 Cánh diều Cho hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O';R'} \right)\) tiếp xúc ngoài nhau tại điểm \(I\). Gọi \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\). Chứng minh \(d\) là tiếp tuyến của \(\left( {O';R'} \right)\). Phương pháp giải: Dựa vào kiến thức vừa học để chứng minh. Lời giải chi tiết:
Vì (O;R) và (O';R') tiếp xúc ngoài nhau tại I nên O, I, O' thẳng hàng và I nằm giữa O và O'. Do \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\) nên \(OI \bot d\) hay \(O'I \bot d\). Mà \(I \in \left( {O'} \right),I \in d\) nên \(d\) là tiếp tuyến của \(\left( {O';R'} \right)\). LT3 Video hướng dẫn giải Trả lời câu hỏi Luyện tập 3 trang 108 SGK Toán 9 Cánh diều Cho hai đường tròn \(\left( O \right),\left( {O'} \right)\) cắt nhau tại hai điểm \(A,B\) sao cho đường thẳng \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\). Chứng minh đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\). Phương pháp giải: Dựa vào các kiến thức vừa học để chứng minh. Lời giải chi tiết:
Do \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\) nên \(O'A \bot OA\). Vậy \(\widehat {OAO'} = 90^\circ \). Xét tam giác \(OAO'\) và tam giác \(OBO'\) có: \(\left\{ \begin{array}{l}O'A = O'B\\OO'\,\,chung\\OA = OB\end{array} \right.\) \(\begin{array}{l} \Rightarrow \Delta OAO' = \Delta OBO'\left( {c.c.c} \right)\\ \Rightarrow \widehat {OAO'} = \widehat {OBO'}\end{array}\). Mà \(\widehat {OAO'} = 90^\circ \) nên \(\widehat {OBO'} = 90^\circ \) hay \(OB \bot O'B\). Vậy đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
|





















Danh sách bình luận