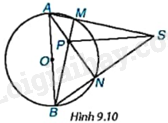
Giải bài tập 9.5 trang 71 SGK Toán 9 tập 2 - Kết nối tri thứcCho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A), N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc với AB. Quảng cáo
Đề bài Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A), N (khác B). Gọi P là giao điểm của BM và AN (H.9.10). Chứng minh rằng SP vuông góc với AB.
Video hướng dẫn giải Phương pháp giải - Xem chi tiết + Sử dụng kiến thức: Góc nội tiếp chắn nửa đường tròn là góc vuông để chỉ ra \(\widehat {AMB} = \widehat {ANB} = {90^o}\) + Chứng minh P là trực tâm của tam giác SAB, suy ra SP là đường cao của tam giác SAB. Do đó, SP vuông góc với AB. Lời giải chi tiết Vì M, N thuộc đường tròn (O) đường kính AB nên \(\widehat {AMB} = \widehat {ANB} = {90^o}\). Do đó, \(BM \bot SA,AN \bot SB\) Suy ra, BM, AN là các đường cao của tam giác SAB. Mà P là giao điểm của BM và AN nên P là trực tâm của tam giác SAB. Suy ra, SP là đường cao của tam giác SAB. Do đó, SP vuông góc với AB.  Chia sẻ Bình luận
Tham Gia Group Dành Cho Học Sinh Lớp 9 - Ôn Thi Vào Lớp 10
|
Danh sách bình luận