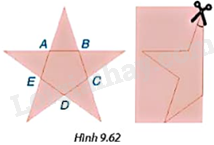
Giải bài tập 9.44 trang 92 SGK Toán 9 tập 2 - Kết nối tri thứcBạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu? Quảng cáo
Đề bài Bạn Lan muốn cắt hình ngôi sao có dạng như Hình 9.62 (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu?
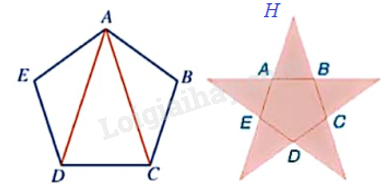
Video hướng dẫn giải Phương pháp giải - Xem chi tiết + Tính được góc trong ngũ giác đều bằng \({108^o}\). + Tính được \(\widehat {HAB} = \widehat {HBA} = {180^o} - {108^o} = {72^o}\) nên \(\widehat {AHB} = {180^o} - \widehat {HAB} - \widehat {HBA} = {180^o} - {72^o} - {72^o} = {36^o}\) + Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng \(\frac{1}{2}\widehat {AHB} = \frac{1}{2}{.36^o} = {18^o}\). Lời giải chi tiết
Xét ngũ giác đều ABCDE, ta thấy tổng 5 góc của ngũ giác đều đó bằng tổng các góc trong ba tam giác ABC, ACD, ADE, tức là bằng \({3.180^o} = {540^o}\). Do tất cả các góc của ngũ giác đều bằng nhau nên số đo mỗi góc của ngũ giác đều bằng \(\frac{{{{540}^o}}}{5} = {108^o}\). Do đó, \(\widehat {EAB} = \widehat {ABC} = {108^o}\). Suy ra: \(\widehat {HAB} = \widehat {HBA} = {180^o} - {108^o} = {72^o}\). Tam giác HAB có: \(\widehat {AHB} = {180^o} - \widehat {HAB} - \widehat {HBA} = {180^o} - {72^o} - {72^o} = {36^o}\) Do đó, góc tạo bởi lưỡi kéo và nếp gấp lúc đầu là: \(\frac{1}{2}\widehat {AHB} = \frac{1}{2}{.36^o} = {18^o}\).
|




















Danh sách bình luận