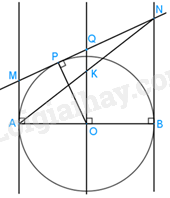
Giải bài tập 5.30 trang 110 SGK Toán 9 tập 1 - Kết nối tri thức

Đề bài

Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (khác A và B) cắt xx’ tại M và cắt yy’ tại N.

a) Chứng minh rằng MN = MA + NB.

b) Đường thẳng đi qua O và vuông góc với AB cắt NM tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.

c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.

Lời giải chi tiết

a) MA và MP là hai tiếp tuyến cắt nhau của (O) nên MA = MP

NB và NP là hai tiếp tuyến cắt nhau của (O) nên NB = NP

Ta có: MN = MP + NP = MA + NB

b) Gọi K là giao điểm của AN và OQ.

Ta có: \({\rm{BN//OK}}\) (vì cùng vuông góc với AB) và O là trung điểm của AB.

Suy ra OK là đường trung bình của tam giác ABN.

Do đó K là trung điểm của AN.

Lại có: \({\rm{AM//QK}}\) (vì cùng vuông góc với AB) và K là trung điểm của AN.

Suy ra QK là đường trung bình của tam giác AMN.

Do đó Q là trung điểm của MN.

c) OK là đường trung bình của tam giác ABN nên \({\rm{OK}} = \frac{1}{2}{\rm{NB}}\)

QK là đường trung bình của tam giác AMN nên \({\rm{QK}} = \frac{1}{2}{\rm{MA}}\)

Suy ra: \({\rm{OQ}} = {\rm{OK}} + {\rm{QK}} = \frac{1}{2}{\rm{NB}} + \frac{1}{2}{\rm{MA}} = \frac{1}{2}{\rm{MN}}\)

hay \({\rm{OQ}} = {\rm{AQ}} = {\rm{BQ}}\)

Do đó O thuộc đường tròn đường kính MN.

Mà OQ vuông góc với AB tại O nên AB là tiếp của đường tròn đường kính MN.