Giải bài tập 4.11 trang 78 SGK Toán 9 tập 1 - Kết nối tri thứcTính các góc của hình thoi có hai đường chéo dài (2sqrt 3 )và 2. Quảng cáo
Đề bài Tính các góc của hình thoi có hai đường chéo dài \(2\sqrt 3 \) và 2. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Hình thoi có hai đường chéo cắt nhau tại trung điểm của mỗi đường, đường chéo là phân giác của góc hình thoi, hai đường chéo vuông góc với nhau, từ đó ta có tam giác vuông và các số đo các cạnh của tam giác đó, để tính tỉ số lượng giác, giải các góc của hình thoi Chú ý: Các góc đối của hình thoi bằng nhau. Lời giải chi tiết
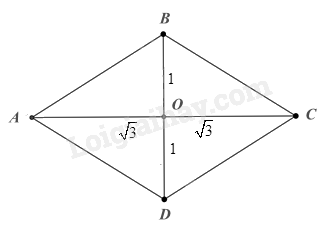
Theo đề bài ta có: \(AC = 2\sqrt3;\; BD = 2\). Gọi giao điểm của hai đường chéo AC và BD là O. Suy ra \(AO = OC = \sqrt3\); \(BO = OD = 1\). Xét tam giác AOB vuông tại O, ta có: \(tan ABO = \frac{AO}{BO}=\frac{\sqrt3}{1} =\sqrt3\) Suy ra \(\widehat{ABO} = 60^\circ\) suy ra \(\widehat{BAO} = 90^\circ - 60^\circ = 30^\circ\) Theo tính chất hình thoi, ta có: \(\widehat{ABC} = 2\widehat{ABO} = 120^\circ\) \(\widehat{BAD} = 2\widehat{BAO} = 60^\circ\) Vậy hình thoi có các góc là \(120^\circ\) và \(60^\circ\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
