Bài 9 trang 202 SBT Hình học 10

Đề bài

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({(x - 5)^2} + {(y - 3)^2} = 4\) . Và điểm A(1 ; 2), một đường thẳng d đi qua A và cắt đường tròn (C) theo một dây cung MN có độ dài bằng \(2\sqrt 3 \) .  Viết phương trình của d.

Lời giải chi tiết

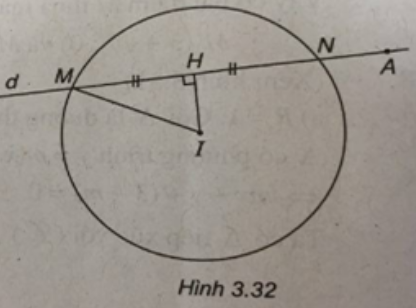
Đường tròn (C) có tâm I(5 ; 3) và có bán kính R = 2.

Gọi H là trung điểm của MN. Ta có

\(IH \bot MN\) và \(MH = \frac{{MN}}{2} = \sqrt 3 \)

\(IH = \sqrt {I{M^2} - M{H^2}}  = \sqrt {4 - 3}  = 1.\)

Phương trình đường thẳng d có dạng :

\(y - 2 = k(x - 1) \) \(\Leftrightarrow kx - y + 2 - k = 0.\)

Ta có IH = 1

\( \Leftrightarrow \frac{{\left| {5k - 3 + 2 - k} \right|}}{{\sqrt {{k^2} + 1} }} = 1\)

\( \Leftrightarrow \left| {4k - 1} \right| = \sqrt {{k^2} + 1}  \) \(\Leftrightarrow {\left( {4k - 1} \right)^2} = {k^2} + 1\)

\( \Leftrightarrow 15{k^2} - 8k = 0 \) \(\Leftrightarrow \left[ \begin{array}{l}k = 0\\k = \frac{8}{{15}}\end{array} \right.\)

Vậy có hai điểm d thỏa mãn đề bài.

Đó là \({d_1}:y - 2 = 0\)

\({d_2}:y - 2 = \frac{8}{{15}}\left( {x - 1} \right)\) \( \Leftrightarrow 8x - 15y + 22 = 0.\)

Loigiaihay.com