Bài 13 trang 202 SBT Hình học 10

Đề bài

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \((x - 1) + {(y - 2)^2} = 4\)  và hai điểm A(1 ; 4),    \(B\left( {1;\frac{1}{2}} \right)\) . Viết phương trình đường thẳng d đi qua B cắt đường tròn (C) tại M, N sao cho AMN có diện tích lớn nhất.

Lời giải chi tiết

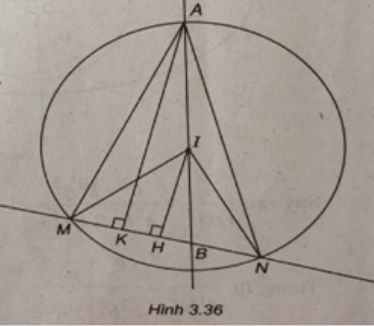
Đường tròn (C) có tâm I(1 ; 2) và có bán kính R = 2.

Ta có \({x_A} = {x_1} = {x_B} = 1\)

Suy ra A, I, B cùng thuộc đường thẳng có phương trình \(x = 1\) .

Ta có \(IA = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( {4 - 2} \right)}^2}}  = 2 = R\)

\(IB = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( {\frac{1}{2} - 2} \right)}^2}}  = \frac{3}{2} < R.\)

Suy ra điểm A nằm trên đường tròn và điểm B nằm trong hình tròn.

Gọi H và K là hình chiếu của I và A xuống đường thẳng d.

Ta có

\(\frac{{{S_{AMN}}}}{{{S_{IMN}}}} = \frac{{AK}}{{IH}} = \frac{{AB}}{{IB}} = \frac{{\frac{7}{2}}}{{\frac{3}{2}}} = \frac{7}{3}.\)

Suy ra \({S_{AMN}} = \frac{7}{3}{S_{IMN}}\)

\( = \frac{7}{3}.\frac{1}{2}.I{\rm{I}}\sin MIN\)

\( = \frac{{14}}{3}\sin MIN \le \frac{{14}}{3}.\)

\({S_{AMN}}\) lớn nhất \( \Leftrightarrow \sin MIN = 1 \Leftrightarrow \widehat {MIN} = {90^ \circ }\)

\( \Leftrightarrow IH = \frac{{R\sqrt 2 }}{2} \Leftrightarrow d(I,MN) = \sqrt 2 \).

Phương trình đường thẳng MN là : \(y - \frac{1}{2} = k(x - 1) \) \(\Leftrightarrow 2kx - 2y + (1 - 2k) = 0.\)

Ta có \(d(I,MN) = \sqrt 2  \Leftrightarrow \frac{{\left| {2k - 4 + 1 - 2k} \right|}}{{\sqrt {4{k^2} + 4} }} = \sqrt 2 \)

\( \Leftrightarrow 3 = \sqrt {8({k^2} + 1)}  \Leftrightarrow k =  \pm \frac{{\sqrt 2 }}{4}.\)

Vậy phương trình đường thẳng d là : \(y =  \pm \frac{{\sqrt 2 }}{4}\left( {x - 1} \right) + \frac{1}{2}\) .

Loigiaihay.com