Bài 9 trang 138 SBT toán 7 tập 1

Đề bài

Cho tam giác \(ABC\) vuông tại \(A.\) Kẻ \(AH\) vuông góc với \(BC\; (H ∈ BC)\). Tìm góc bằng góc \(B.\)

Lời giải chi tiết

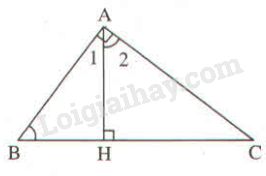
Có thể tìm góc bằng góc \(B\) bằng hai cách: 

*Cách 1

Ta có \(\widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAC} = 90^\circ \)         (1)

Xét \(∆AHB\) vuông tại \(H\) nên ta có:

\(\widehat B + \widehat {A_1} = 90^\circ \) (tính chất tam giác vuông)         (2)

Từ (1) và (2) suy ra: \(\widehat B = \widehat {{A_2}}\)

*Cách 2

Xét \(∆ABC\) vuông tại \(A\) nên ta có: 

\(\widehat B + \widehat C = 90^\circ \) (tính chất tam giác vuông)             (3)

Xét \(∆AHC\) vuông tại \(H\) nên ta có:

\(\widehat {{A_2}} + \widehat C = 90^\circ \) (tính chất tam giác vuông)          (4)

Từ (3) và (4) suy ra: \(\widehat B = \widehat {{A_2}}\).

Loigiaihay.com