Bài 10 trang 138 SBT toán 7 tập 1

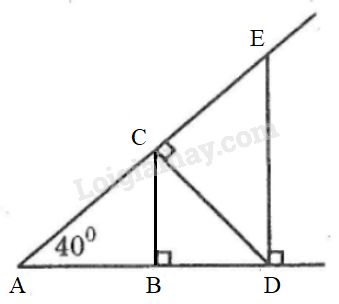
Đề bài

Cho hình 48:

a) Có bao nhiêu tam giác vuông trong hình?

b) Tính số đo các góc nhọn ở các đỉnh \(C, D, E.\)

Lời giải chi tiết

a) Có năm tam giác vuông trong hình:

               \(∆ABC\) vuông tại \(B\)

               \(∆CBD\) vuông tại \(B\)

               \(∆EDA\) vuông tại \(D\)

               \(∆DCA\) vuông tại \(C\)

               \(∆DCE\) vuông tại \(C\)

b) \(∆ABC\) vuông tại \(B\), suy ra:

\(\widehat A + \widehat {ACB} = 90^\circ \) (tính chất tam giác vuông)

\( \Rightarrow \widehat {ACB} = 90^\circ - \widehat A = 90^\circ - 40^\circ \)\(\,= 50^\circ \)

\( \widehat {ACB} + \widehat {BC{\rm{D}}} = \widehat {AC{\rm{D}}} = 90^\circ \)

\( \Rightarrow \widehat {BC{\rm{D}}} = 90^\circ - \widehat {ACB} = 90^\circ - 50^\circ\)\(\, = 40^\circ \)

\(∆ACD\) vuông tại \(C\), suy ra:

\(\widehat A + \widehat {C{\rm{D}}A} = 90^\circ \) (tính chất tam giác vuông)

\( \Rightarrow \widehat {C{\rm{D}}A} = 90^\circ - \widehat A = 90^\circ - 40^\circ \)\(\,= 50^\circ \)

\( \widehat {C{\rm{D}}A} + \widehat {C{\rm{D}}E} = \widehat {A{\rm{D}}E} = 90^\circ \)

\( \Rightarrow \widehat {C{\rm{D}}E} = 90^\circ - \widehat {C{\rm{D}}A} = 90^\circ - 50^\circ\)\(\, = 40^\circ  \)

\(∆DEA\) vuông tại \(D\), suy ra:

\(\widehat A + \widehat E = 90^\circ \) (tính chất tam giác vuông)

\( \Rightarrow \widehat E = 90^\circ  - \widehat A = 90^\circ  - 40^\circ  = 50^\circ \)

Loigiaihay.com