Bài 12 trang 138 SBT toán 7 tập 1

Đề bài

Cho tam giác \(ABC.\) Các tia phân giác của các góc \(B\) và \(C\) cắt nhau ở \(I.\) Tính \(\widehat {BIC}\) biết rằng:

a) \({\rm{}}\widehat B = 80^\circ ,\widehat C = 40^\circ \)

b) \(\widehat A = 80^\circ \)

c) \(\widehat A = m^\circ \)

Lời giải chi tiết

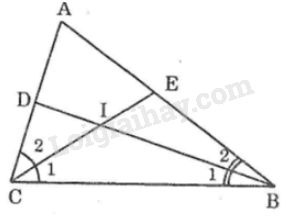
Gọi D là giao điểm của BI với AC, E là giao điểm của CI với AB.

a) Ta có 

\(\displaystyle \widehat {{B_1}} = {1 \over 2}\widehat {ABC} = {1 \over 2}.80^\circ  = 40^\circ \) (vì \(BD\) là tia phân giác của \(\widehat {ABC}\))

\(\displaystyle \widehat {{C_1}} = {1 \over 2}\widehat {ACB} = {1 \over 2}.40^\circ  = 20^\circ \) (vì \(CE\) là tia phân giác của \(\widehat {ACB}\))

Trong \(∆IBC\), ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng ba góc của một tam giác)

\(\Rightarrow \widehat {BIC} = {180^\circ } - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) \)\(\,= 180^\circ  - \left( {40^\circ  + 20^\circ } \right) = 120^\circ \)

b) Ta có:

\(\displaystyle \widehat {{B_1}} = {1 \over 2}\widehat B\) (vì \(BD\) là tia phân giác \(\widehat B\))

\(\displaystyle \widehat {{C_1}} = {1 \over 2}\widehat C\) (vì \(CE\) là tia phân giác \(\widehat C\))

Suy ra \(\widehat {{B_1}} + \widehat {{C_1}}=\displaystyle {{\widehat B + \widehat C} \over 2}\)

Trong \(∆ABC\), ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc của một tam giác)

Suy ra \(\widehat B + \widehat C = 180^\circ  - \widehat A = 180^\circ  - 80^\circ  \)\(\,= 100^\circ \)

Trong \(∆IBC\), ta có: \(\widehat {BIC} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \)

\( \Rightarrow \widehat {BIC} = 180^\circ  - \left( {\widehat {{B_1}} + \widehat {{C_1}}} \right) \)\(\,\displaystyle = 180^\circ  - {{\widehat B + \widehat C} \over 2} = 180^\circ  - {{100^\circ } \over 2} \)\(\,= 130^\circ \)

c) 

Trong \(∆ABC\), ta có:

\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc của một tam giác)

Suy ra \(\widehat B + \widehat C = 180^\circ  - \widehat A = 180^\circ  - m^\circ  \)

Theo câu b) ta có: \( \displaystyle \widehat {BIC} = 180^\circ  - {{\widehat B + \widehat C} \over 2} \)

Nên \(\displaystyle\widehat {BIC} = 180^\circ  - {{180^\circ  - m^\circ } \over 2} \)\(\,\displaystyle = 180^\circ  - 90^\circ  + {{m^\circ } \over 2} = 90^\circ  + {{m^\circ } \over 2}\)

Loigiaihay.com