Bài 8 trang 138 SBT toán 7 tập 1Giải bài 8 trang 138 sách bài tập toán 7 tập 1. Cho tam giác ABC có góc A = 100^o ... Quảng cáo
Đề bài Cho tam giác \(ABC\) có \(\widehat A = 100^\circ ,\widehat B - \widehat C = 20^\circ \). Tính \(\widehat B\) và \(\widehat C\). Phương pháp giải - Xem chi tiết Định lí: Tổng ba góc của một tam giác bằng \({180^0}\) Lời giải chi tiết
Áp dụng định lí tổng ba góc của một tam giác vào \(∆ABC\), ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) \( \Rightarrow \widehat B + \widehat C = {180^o} - \widehat A\) \( \Rightarrow \widehat B + \widehat C = 180^\circ - 100^\circ \) \( \Rightarrow \widehat B + \widehat C = 80^\circ \) (1) \(\widehat B - \widehat C = 20^\circ \left( {gt} \right)\) (2) Cộng (1) và (2) theo vế với vế ta được: \(\widehat B + \widehat C +\widehat B - \widehat C \)\(=80^0+20^0=100^0\) \(\Rightarrow 2\widehat B = 100^\circ \Rightarrow \widehat B =100^\circ :2= 50^\circ \) Vậy \(\widehat C = 80^\circ - 50^\circ = 30^\circ \). Loigiaihay.com
|














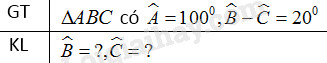






Danh sách bình luận