Bài 79 trang 148 SBT toán 7 tập 1

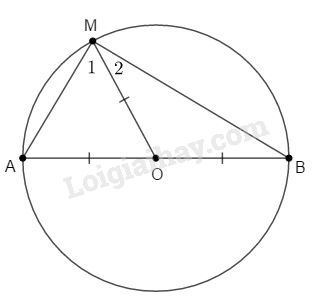
Đề bài

Cho đường tròn tâm \(O\) đường kính \(AB.\) Gọi \(M\) là một điểm nằm trên đường tròn, tính số đo góc \(AMB\).

Lời giải chi tiết

Nối \(OM\), ta có:

\(OA = OM\) (bằng bán kính đường tròn tâm \(O\)) 

\( \Rightarrow ∆OAM\) cân tại \(O\).

\( \Rightarrow \widehat A = \widehat {{M_1}}\) (tính chất tam giác cân)  (1)

\(OM = OB\) (bằng bán kính đường tròn tâm \(O\))

\( \Rightarrow  ∆OBM\) cân tại \(O\).

\( \Rightarrow \widehat {{M_2}} = \widehat B\) (tính chất tam giác cân)  (2)

Áp dụng định lí tổng các góc của một tam giác vào \(∆AMB\), ta có:

\(\widehat A + \widehat {AMB} + \widehat B = 180^\circ \)

\( \Rightarrow \widehat A + \widehat {{M_1}} + \widehat {{M_2}} + \widehat B = 180^\circ \)       (3)

Từ (1), (2) và (3) suy ra:

\(  \widehat M_1 + \widehat {{M_1}} + \widehat {{M_2}} + \widehat M_2 = 180^\circ \)

\(\Rightarrow 2.\left( {\widehat {{M_1}} + \widehat {{M_2}}} \right) = 180^\circ \)

\( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} =180^o:2= 90^\circ \) hay \(\widehat {AMB} = 90^\circ \)

Loigiaihay.com