Bài 77 trang 148 SBT toán 7 tập 1Giải bài 77 trang 148 sách bài tập toán 7 tập 1. Cho tam giác đều ABC. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Quảng cáo
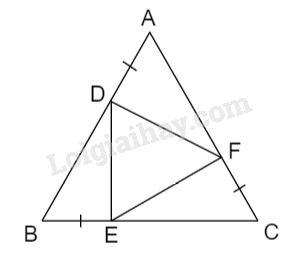
Đề bài Cho tam giác đều \(ABC.\) Lấy các điểm \(D, E, F\) theo thứ tự thuộc các cạnh \(AB, BC, CA\) sao cho \(AD = BE = CF.\) Chứng minh rằng \(∆DEF\) là tam giác đều. Phương pháp giải - Xem chi tiết Sử dụng: - Tam giác đều là tam giác có ba cạnh bằng nhau. - Tính chất: Tam giác đều có ba góc bằng nhau và cùng bằng \(60^o\). Lời giải chi tiết
Ta có: \(AB = AD + DB\) (1) \(BC = BE + EC\) (2) \(AC = AF + FC\) (3) \(AB = AC = BC\) (vì tam giác ABC là tam giác đều) (4) \(AD = BE = CF\) (gt) (5) Từ (1), (2), (3), (4) và (5) suy ra: \(BD = EC = AF\) Xét \(∆ADF\) và \(∆BED\) có: \( AD = BE \) (gt) \(\widehat A = \widehat B = 60^\circ \) (vì \(∆ABC\) đều) \(AF = BD\) (chứng minh trên) \( \Rightarrow ∆ADF = ∆BED \) (c.g.c) \( \Rightarrow DF = ED\) (hai cạnh tương ứng) (6) Xét \(∆ADF\) và \(∆CFE\) có: \( AD = CF\) (gt) \(\widehat A = \widehat C = 60^\circ \) (vì \(∆ABC\) đều) \( AF=EC\) (chứng minh trên) \( \Rightarrow ∆ADF = ∆CFE\) (c.g.c) \( \Rightarrow DF = FE\) (hai cạnh tương ứng) (7) Từ (6) và (7) suy ra: \(DF = ED = FE\). Vậy \(∆DEF\) đều. Loigiaihay.com
|














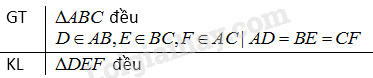






Danh sách bình luận