Bài 77 trang 51 SBT toán 7 tập 2Giải bài 77 trang 51 sách bài tập toán 7. Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của ∆ABC, đường cao AF của ∆ACD... Quảng cáo
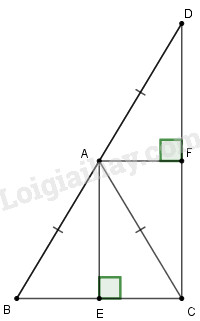
Đề bài Cho tam giác \(ABC \) cân tại \(A.\) Vẽ điểm \(D\) sao cho \(A\) là trung điểm của \(BD.\) Kẻ đường cao \(AE\) của \(∆ABC,\) đường cao \(AF\) của \(∆ACD.\) Chứng minh rằng \(\widehat {EAF} = 90^\circ \) Phương pháp giải - Xem chi tiết Sử dụng: +) Trong một tam giác cân, đường trung tuyến ứng với cạnh đáy cũng đồng thời là đường phân giác của tam giác đó. +) Hai góc kề bù có tổng bằng \(180^0.\) Lời giải chi tiết
Vì \(∆ABC\) cân tại \(A,\) có \(A{\rm{E}} \bot BC\left( {gt} \right)\) Hay \(AE\) là đường cao, suy ra \(AE\) cũng là đường phân giác của \(\widehat {BAC}\) \( \Rightarrow \widehat {EAC} = \dfrac{1}{2}\widehat {BAC}\) (1) Vì \(∆ABC\) cân tại \(A\) nên \(AB=AC\) mà \(AB=AD\) (vì A là trung điểm BD), suy ra: \(AD=AC=AB\) nên \(∆ADC\) cân tại \(A.\) Vì \(∆ADC\) cân tại \(A,\) có \({\rm{AF}} \bot {\rm{DC}}\left( {gt} \right)\) Hay\(AF\) là đường cao, suy ra \(AF\) cũng là đường phân giác của \(\widehat {CA{\rm{D}}}\) \( \Rightarrow \widehat {FAC} = \dfrac{1}{2}\widehat {DAC}\) (2) Mà \(\widehat {BAC}\) và \(\widehat {CA{\rm{D}}}\) là hai góc kề bù nên \(\widehat {BAC} + \widehat {DAC}=180^0\) (3) Từ (1), (2), (3) ta có: \(\widehat {EAC} + \widehat {FAC} \)\(= \dfrac{1}{2}\left( {\widehat {BAC} + \widehat {DAC}} \right) \)\(= \dfrac{1}{2}.180^\circ = 90^\circ \) Hay \(\widehat {EAF} = 90^\circ \) Suy ra: \(A{\rm{E}} \bot {\rm{AF}}\) Loigiaihay.com
|














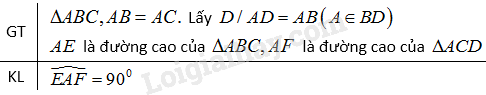






Danh sách bình luận