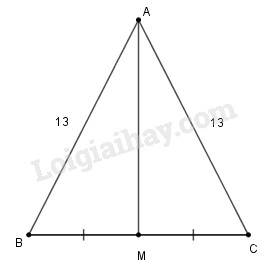
Bài 79 trang 51 SBT toán 7 tập 2

Đề bài

Cho tam giác \(ABC\) có \(AB = AC = 13cm, BC = 10cm.\) Tính độ dài đường trung tuyến \(AM.\) 

Lời giải chi tiết

Vì \(∆ABC\) cân tại \(A\) (do \(AB=AC=13cm\)) nên đường trung tuyến \(AM\) cũng là đường cao. 

\( \Rightarrow AM \bot BC\)

Ta có: \(\displaystyle MB = MC = {1 \over 2}BC = 5\left( {cm} \right)\)

Trong tam giác vuông \(AMB\) có \(\widehat {AMB} = 90^\circ \)

Theo định lý Pytago ta có:  

\(A{B^2} = A{M^2} + M{B^2}\)

\(\eqalign{
& \Rightarrow A{M^2} = A{B^2} - M{B^2} = {13^2} - {5^2} \cr 
& = 169 - 25 = 144 \cr 
&\Rightarrow AM = 12\left( {cm} \right) \cr} \)

Loigiaihay.com