Bài 74 trang 51 SBT toán 7 tập 2Giải bài 74 trang 51 sách bài tập toán 7. Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC. Quảng cáo
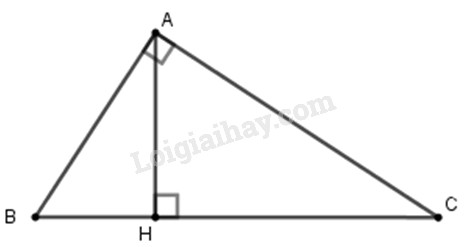
Đề bài Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Tìm trực tâm của tam giác \(ABC, AHB, AHC.\) Phương pháp giải - Xem chi tiết Sử dụng: Ba đường cao của tam giác cùng đi qua một điểm. Điểm đó gọi là trực tâm của tam giác. Lời giải chi tiết
Xét \(∆ABC\) có \(\widehat {BAC} = 90^\circ \) nên \(AB \bot AC\) Do đó, \(CA\) là đường cao xuất phát từ đỉnh \(C,\) \(BA\) là đường cao xuất phát từ đỉnh \(B.\) Giao điểm của hai đường này là \(A.\) Vậy \(A\) là trực tâm của \(∆ABC.\) Xét \(∆AHB\) có \(AH \bot HB \) Do đó, \(AH\) là đường cao xuất phát từ đỉnh \(A,\) \(BH\) là là đường cao xuất phát từ đỉnh \(B.\) Giao điểm của hai đường này là \(H.\) Vậy \(H\) là trực tâm của \(∆AHB\) Xét \(∆AHC\) có \(AH \bot HC\) Do đó, \(AH\) là đường cao xuất phát từ đỉnh \(A,\) \(CH\) là đường cao xuất phát từ đỉnh \(C.\) Giao điểm của hai đường này là \(H\) Vậy \(H\) là trực tâm của \(∆AHC.\) Loigiaihay.com
|














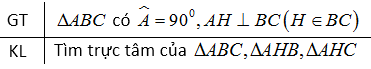






Danh sách bình luận