Bài 59 trang 145 SBT toán 7 tập 1

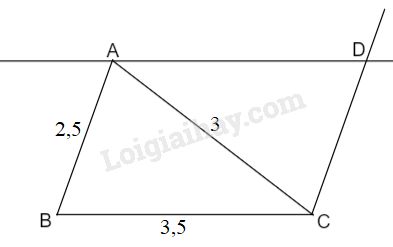
Đề bài

Cho tam giác \(ABC\) có \(AB = 2,5cm, AC = 3cm, \) \(BC = 3,5cm.\) Qua \(A\) vẽ đường thẳng song song với \(BC\), qua \(C\) vẽ đường thẳng song song với \( AB\), chúng cắt nhau ở \(D.\) Tính chu vi tam giác \(ACD.\)

Lời giải chi tiết

Vì \(AB // CD\) (gt) nên \(\widehat {AC{\rm{D}}} = \widehat {CAB}\) (hai góc so le trong)

Vì \(BC // AD\) (gt) nên \(\widehat {{\rm{CAD}}} = \widehat {ACB}\) (hai góc so le trong)

Xét \(∆ABC\) và \(∆CDA\) có: 

\(  \widehat {CAB}=\widehat {AC{\rm{D}}}\) (chứng minh trên)

\(AC\) cạnh chung

\( \widehat {ACB}=\widehat {CA{\rm{D}}}\) (chứng minh trên)

\( \Rightarrow   ∆ABC = ∆CDA\) (g.c.g)

\( \Rightarrow CD = AB = 2,5(cm);\) \(AD = BC = 3,5 (cm)\) (các cạnh tương ứng).

Chu vi \(∆ACD\) là: \(AC + AD + CD = 3 + 3,5 + 2,5 \)\(\,= 9 (cm)\).

Loigiaihay.com