Bài 4.44 trang 113 SBT đại số 10

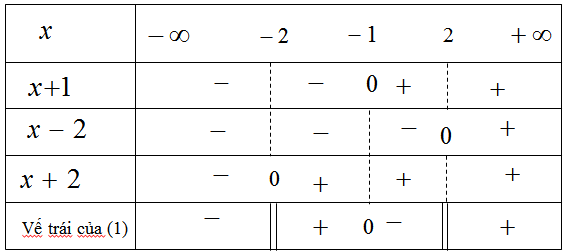
Đề bài

Nghiệm của bất phương trình \(\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\) là

A. \( - 2 < x \le 1;x > 2\)

B. \( - 2 < x \le 1\);\(x \ge 2\)

C. \(x \le  - 2; - 1 \le x \le 2\)

D. \(x \le  - 2\);\( - 1 \le x < 2\)

Lời giải chi tiết

Điều kiện \({x^2} - 4 \ne 0\)\( \Leftrightarrow x \ne  \pm 2\)

\(\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\)\( \Leftrightarrow \dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} - 1 \ge 0\)

\( \Leftrightarrow \dfrac{{x + 1}}{{(x - 2)(x + 2)}} \ge 0\)

\(f(x) = 0\)\( \Leftrightarrow \dfrac{{x + 1}}{{(x - 2)(x + 2)}} = 0\)\( \Leftrightarrow x + 1 = 0\)\( \Leftrightarrow x =  - 1\)

Ta có bảng xét dấu

Nhìn vào bảng xét dấu ta thấy

\(f(x) \ge 0\) khi \( - 2 < x \le  - 1,x > 2\)

Đáp án A.

Loigiaihay.com