Bài 4.42 trang 113 SBT đại số 10Giải bài 4.42 trang 113 sách bài tập đại số 10. Giải bất phương trình sau... Quảng cáo
Đề bài Giải bất phương trình sau \(|x + 2| + \left| { - 2x + 1} \right| \le x + 1\). Phương pháp giải - Xem chi tiết - Phá bỏ trị tuyệt đối - Lập bảng xét dấu - Dựa vào bảng xét dấu, giải bất phương trình tương ứng Lời giải chi tiết Bỏ dấu giá trị tuyệt đối ở vế trái của bất phương trình ta có:
Bất phương trình đã cho tương đương với \(\left[ \begin{array}{l}\left\{ \begin{array}{l}x \le - 2\\ - (x + 2) + ( - 2x + 1) \le x + 1\end{array} \right.\\\left\{ \begin{array}{l} - 2 < x \le \dfrac{1}{2}\\(x + 2) + ( - 2x + 1) \le x + 1\end{array} \right.\\\left\{ \begin{array}{l}x > \dfrac{1}{2}\\(x + 2) - ( - 2x + 1) \le x + 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \le - 2\\4x \ge - 2\end{array} \right.\\\left\{ \begin{array}{l} - 2 < x \le \dfrac{1}{2}\\2x \ge 2\end{array} \right.\\\left\{ \begin{array}{l}x > \dfrac{1}{2}\\2x \le 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \le - 2\\x \ge - \dfrac{1}{2}\end{array} \right.\\\left\{ \begin{array}{l} - 2 < x \le \dfrac{1}{2}\\x \ge 1\end{array} \right.\\\left\{ \begin{array}{l}x > \dfrac{1}{2}\\x \le 0\end{array} \right.\end{array} \right.\)(Vô nghiệm) Vậy bất phương trình đã cho vô nghiệm. Loigiaihay.com
|














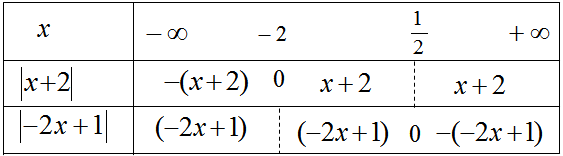






Danh sách bình luận