Bài 4.36 trang 112 SBT đại số 10

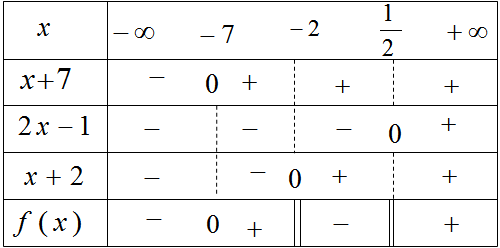
Đề bài

Xét dấu biểu thức sau:

\(f(x) = \dfrac{3}{{2x - 1}} - \dfrac{1}{{x + 2}}\)

Lời giải chi tiết

Điều kiện để f(x) có nghĩa:

\(\left\{ \begin{array}{l}
2x - 1 \ne 0\\
x + 2 \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x \ne \dfrac{1}{2}\\
x \ne - 2
\end{array} \right.\)

\(f(x) = \dfrac{{3(x + 2) - (2x - 1)}}{{(2x - 1)(x + 3)}} \) \(= \dfrac{{x + 7}}{{(2x - 1)(x + 2)}}\)

\(f(x) = 0\)\( \Leftrightarrow \dfrac{{x + 7}}{{(2x - 1)(x + 2)}} = 0\)\( \Leftrightarrow x + 7 = 0\)\( \Leftrightarrow x =  - 7\)

Ta có bảng xét dấu:

Nhìn vào bảng xét dấu ta thấy

\(f(x) > 0\) khi \(x \in ( - 7; - 2)\) hoặc \(x \in (\dfrac{1}{2}; + \infty )\)

\(f(x) < 0\) khi \(x \in ( - \infty ; - 7)\) hoặc \(x \in ( - 2; \dfrac{1}{2} )\)

\(f(x) = 0\) khi \(x =  - 7\)

\(f(x)\) không xác định khi \(x =  - 2,x = \dfrac{1}{2}\)

Loigiaihay.com