Bài 41 trang 112 SBT toán 7 tập 1

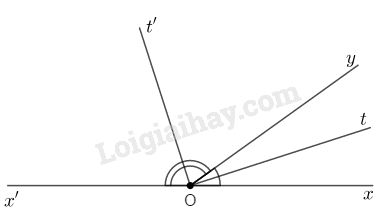
Đề bài

Với hai góc kề bù, ta có định lí sau: 

Hai tia phân giác của hai góc kề bù tạo thành một góc vuông.

a) Hãy vẽ hai góc \(xOy\) và \(yOx'\) kề bù, tia phân giác \(Ot\) của góc \(xOy\), tia phân giác \(Ot'\) của góc \(yOx'\) và gọi số đo của góc \(xOy\) là \(m^\circ \).

b) Hãy viết giả thiết và kết luận của định lí.

c) Hãy điền vào chỗ trống (…) và sắp xếp bốn câu sau đây một cách hợp lý để chứng minh định lí trên:

\(1.\widehat {tOy} = \displaystyle {1 \over 2}m^\circ \) vì ……

\(2.\widehat {t'Oy} = \displaystyle {1 \over 2}(180^\circ  - m^\circ )\) vì ……

\(3.\widehat {tOt'} = 90^\circ \) vì ……

\(4.\widehat {x'Oy} = 180^\circ  - m^\circ \) vì ……

Lời giải chi tiết

a) Hình vẽ:

b)

c) \(\widehat {x'Oy} = 180^\circ  - m^\circ \) (vì \(\widehat {x'Oy}\) và \(\widehat {{\rm{yOx}}}\) kề bù) 

\(\widehat {tOy} = \displaystyle {1 \over 2}m^\circ \) (vì \(Ot\) là tia phân giác của \(\widehat {xOy}\))

\(\widehat {t'Oy} =\displaystyle  {1 \over 2}\left( {180^\circ  - m^\circ } \right)\) (vì \(Ot'\) là tia phân giác của \(\widehat {yOx'}\))

\(\widehat {tOt'} = 90^\circ \) (vì \(\widehat {tOt'} = \widehat {tOy} + \widehat {t'Oy} \)\(\,= \dfrac{1}{2}{m^o} + \dfrac{1}{2}\left( {{{180}^o} - {m^o}} \right) = {90^o}\)).

Kết luận: Vậy hai tia phân giác của hai góc kề bù tạo thành góc vuông.

Loigiaihay.com