Bài 3.62 trang 168 SBT hình học 10

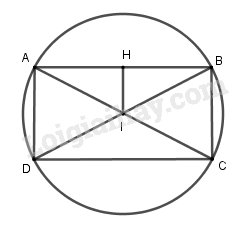
Đề bài

Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có tâm \(I\left( {\dfrac{1}{2};0} \right)\), phương trình đường thẳng AB là : \(x - 2y + 2 = 0\) và AB = 2AD. Tìm tọa độ các đỉnh A, B, C, D biết rằng đỉnh A có hoành độ âm.

Lời giải chi tiết

Khoảng cách từ I đến đường thẳng AB là \(IH = d\left( {I,AB} \right) = \dfrac{{\left| {\dfrac{1}{2} - 2.0 + 2} \right|}}{{\sqrt {{1^2} + {2^2}} }}\) \( = \dfrac{{\sqrt 5 }}{2}\)

\( \Rightarrow AD =2IH= \sqrt 5 \) và \( \Rightarrow AB = 2AD = 2\sqrt 5 \) \( \Rightarrow BD = \sqrt {A{B^2} + A{D^2}}  = 5\) \(   \Rightarrow IA = IB = \dfrac{1}{2}BD = \dfrac{5}{2}\)

Do đó A, B là các giao điểm của đường thẳng AB với đường tròn tâm I và bán kính \(R = \dfrac{5}{2}.\)

Phương trình đường tròn \({\left( {x - \dfrac{1}{2}} \right)^2} + {y^2} = \dfrac{{25}}{4}\)

Vậy tọa độ A, B là nghiệm của hệ :

\(\left\{ \begin{array}{l}x - 2y + 2 = 0\\{\left( {x - \dfrac{1}{2}} \right)^2} + {y^2} = { {\dfrac{25}{4}} }\end{array} \right.\) 

\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
x = 2y - 2\\
{\left( {2y - 2 - \dfrac{1}{2}} \right)^2} + {y^2} = \dfrac{{25}}{4}
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 2y - 2\\
{\left( {2y - \dfrac{5}{2}} \right)^2} + {y^2} = \dfrac{{25}}{4}
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 2y - 2\\
4{y^2} - 10y + \dfrac{{25}}{4} + {y^2} = \dfrac{{25}}{4}
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 2y - 2\\
5{y^2} - 10y = 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 2y - 2\\
\left[ \begin{array}{l}
y = 0\\
y = 2
\end{array} \right.
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
y = 0,x = - 2\\
y = 2,x = 2
\end{array} \right.
\end{array}\)

Do đó \(A( - 2;0),B(2;2)\) (vì \({x_A} < 0\) )

\(I\) là trung điểm \(AC\) \( \Rightarrow \left\{ \begin{array}{l}{x_C} = 2{x_I} - {x_A} = 2.\frac{1}{2} + 2 = 3\\{y_C} = 2{y_I} - {y_A} = 2.0 - 0 = 0\end{array} \right.\) \( \Rightarrow C\left( {3;0} \right)\)

\(I\) là trung điểm \(BD\) \( \Rightarrow \left\{ \begin{array}{l}{x_D} = 2{x_I} - {x_B} = 2.\frac{1}{2} - 2 =  - 1\\{y_D} = 2{y_I} - {y_B} = 2.0 - 2 =  - 2\end{array} \right.\) \( \Rightarrow D\left( { - 1; - 2} \right)\)

Loigiaihay.com