Bài 2.19 trang 71 SBT hình học 11

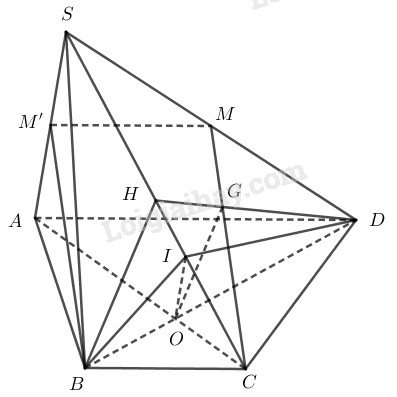
LG a

Chứng minh rằng \(OG\parallel \left( {SBC} \right)\).

Phương pháp giải:

Sử dụng định lý Talet.

Sử dụng tính chất của trọng tâm.

Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song \((\alpha)\).

Lời giải chi tiết:

Tứ giác \(ABCD\) là hình thang có \(AD\parallel =2BC\).

Theo định lý Talet \(\dfrac{OD}{OB}=\dfrac{OA}{OC}=\dfrac{AD}{BC}=2\)

\(\Rightarrow \dfrac{OD}{BD}=\dfrac{OD}{OB+OD}\) \(=\dfrac{2}{1+2}=\dfrac{2}{3}\text{(1)}\).

Gọi \(H\) là trung điểm của \(SC\), tam giác \(SCD\) có \(G\) là trọng tâm nên \(\dfrac{DG}{DH}=\dfrac{2}{3}\text{(2)}\).

Từ \(\text{(1)}\) và \(\text{(2)}\) suy ra \(\dfrac{DO}{DB}=\dfrac{DG}{DH}=\dfrac{2}{3}\)

Theo định lý Talet \(OG\parallel BH\text{(*)}\).

Mà \(H\in SC\Rightarrow H\in (SBC)\)

\(\Rightarrow BH\subset (SBC)\text{(**)}\)

Từ \(\text{(*)}\) và \(\text{(**)}\) suy ra \( OG\parallel (SBC)\).

Quảng cáo

LG b

Cho \(M\) là trung điểm của \(SD\). Chứng minh rằng \(CM\parallel \left( {SAB} \right)\).

Phương pháp giải:

Sử dụng tính chất đường trung bình trong tam giác.

Sử dụng tính chất hình bình hành.

Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song \((\alpha)\).

Lời giải chi tiết:

Gọi \(M’\) là trung điểm của \(SA\) và ta có \(M\) là trung điểm \(SD\) nên trong tam giác \(SAD\) khi đó \(MM’\) là đường trung bình.

\(\Rightarrow MM’\parallel =\dfrac{1}{2}AD\)

Mà hình thang \(ABCD\) có \(BC\parallel =\dfrac{1}{2}AD\)

Suy ra \(MM’\parallel =BC\) \(\Rightarrow\) tứ giác \(MM’BC\) là hình bình hành.

\(\Rightarrow MC\parallel M’B\)

Ta lại có \(M’B\subset (SAB)\)

\(\Rightarrow MC\parallel (SAB)\).

LG c

Giả sử điểm \(I\) nằm trong đoạn \(SC\) sao cho \(S{\rm{C = }}\dfrac{3 }{2}SI\). Chứng minh rằng \(SA\parallel \left( {BI{\rm{D}}} \right)\). 

Phương pháp giải:

Sử dụng định lý Talet.

Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song \((\alpha)\).

Lời giải chi tiết:

Ta có: \(SC=\dfrac{3}{2}SI\) \(\Rightarrow \dfrac{CI}{CS}=\dfrac{1}{3}\).

Mà \(\dfrac{OC}{OA}=\dfrac{BC}{AD}=\dfrac{1}{2}\) nên \(\dfrac{CO}{CA}=\dfrac{1}{3}\).

Suy ra \(\dfrac{CI}{CS}=\dfrac{CO}{CA}=\dfrac{1}{3}\)

Theo định lý Talet ta được \(IO\parallel SA\) mà \(IO\subset (BID)\)

\(\Rightarrow SA\parallel (BID)\).

Loigiaihay.com