Bài 2.10 trang 35 SBT đại số 10

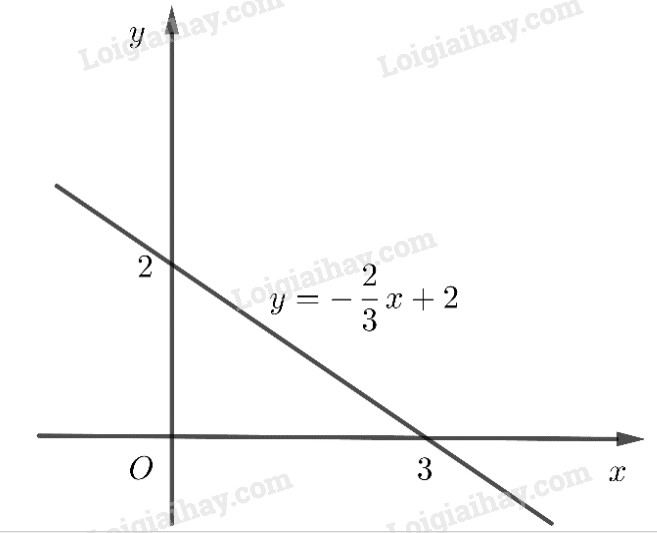
LG a

 \(y =  - \dfrac{2}{3}x + 2\) ;

Phương pháp giải:

Áp dụng cách vẽ đồ thị hàm số \(y = ax + b\) đã được học ở lớp 7 và sử dụng tính chất đồ thị của hàm số chẵn, hàm số lẻ.

Lời giải chi tiết:

Cho \(x=0\) thì \(y=2\), \(y=0\) thì \(x=3\) nên đồ thị đi qua hai điểm \(A(0;2)\) và \(B(3;0)\).

Hàm số không là hàm số chẵn, không là hàm số lẻ vì:

\(\begin{array}{l}
f\left( 1 \right) = - \frac{2}{3}.1 + 2 = \frac{4}{3}\\
f\left( { - 1} \right) = - \frac{2}{3}.\left( { - 1} \right) + 2 = \frac{8}{3}
\end{array}\)

Ta thấy \(f\left( -1 \right) \ne f\left( {  1} \right)\) và \(f\left( -1 \right) \ne - f\left( {  1} \right)\) nên hàm số không chẵn không lẻ.

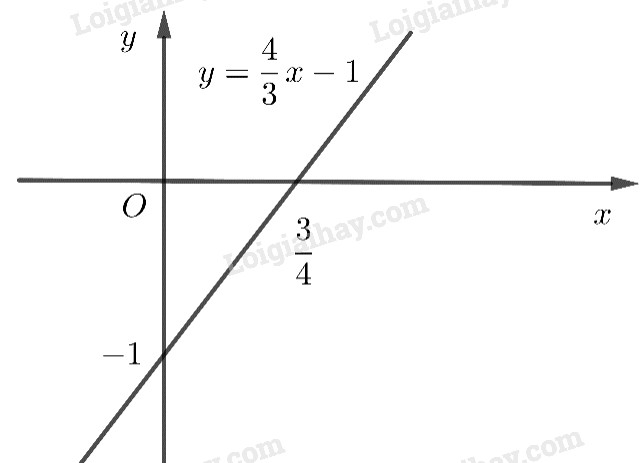
LG b

\(y = \dfrac{4}{3}x - 1\) ;

Phương pháp giải:

Áp dụng cách vẽ đồ thị hàm số \(y = ax + b\) đã được học ở lớp 7 và sử dụng tính chất đồ thị của hàm số chẵn, hàm số lẻ.

Lời giải chi tiết:

Cho \(x=0\) thì \(y=-1\), \(y=0\) thì \(x=\dfrac{3}{4}\) nên đồ thị đi qua hai điểm \(A(0;-1)\) và \(B(\dfrac{3}{4};0)\).

Hàm số không là hàm số chẵn, không là hàm số lẻ vì:

\(\begin{array}{l}
f\left( 1 \right) = \frac{4}{3}.1 - 1 = \frac{1}{3}\\
f\left( { - 1} \right) = \frac{4}{3}.\left( { - 1} \right) - 1 = - \frac{7}{3}\\
f\left( -1 \right) \ne f\left( {  1} \right);f\left( -1 \right) \ne - f\left( {  1} \right)
\end{array}\)

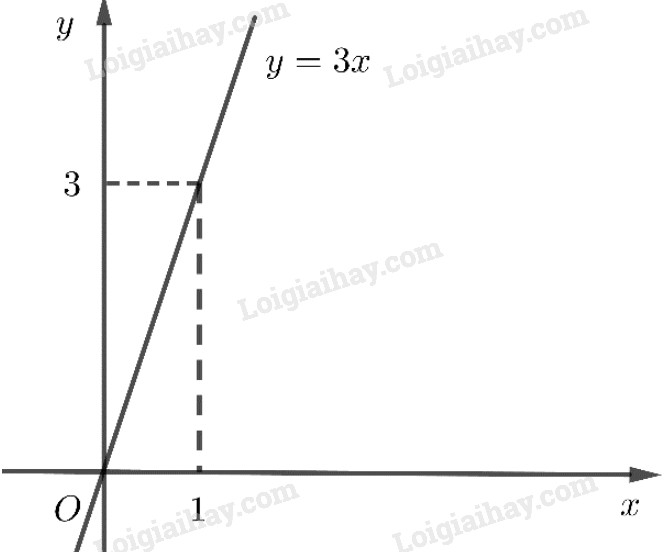
LG c

\(y = 3x\) ;

Phương pháp giải:

Áp dụng cách vẽ đồ thị hàm số \(y = ax + b\) đã được học ở lớp 7 và sử dụng tính chất đồ thị của hàm số chẵn, hàm số lẻ.

Lời giải chi tiết:

 Cho \(x=0\) thì \(y=0\), \(y=3\) thì \(x=1\) nên đồ thị đi qua hai điểm \(A(0;0)\) và \(B(1;3)\).

Hàm số là hàm số lẻ vì TXĐ: D=R và

\(f\left( { - x} \right) = 3.\left( { - x} \right) =  - 3x =  - f\left( x \right)\)

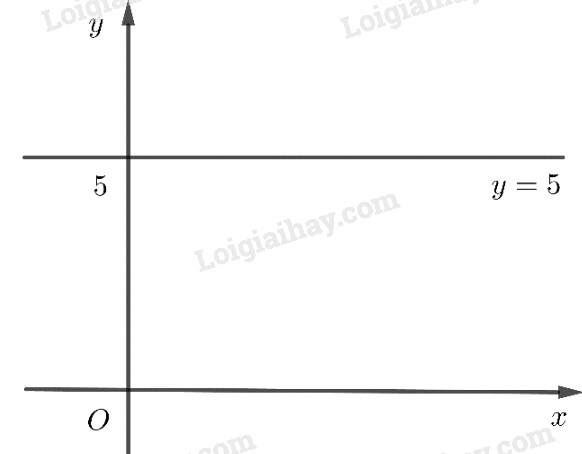
LG d

 \(y = 5\) ;

Phương pháp giải:

Áp dụng cách vẽ đồ thị hàm số \(y = ax + b\) đã được học ở lớp 7 và sử dụng tính chất đồ thị của hàm số chẵn, hàm số lẻ.

Lời giải chi tiết:

Cho \(x=0\) thì \(y=5\), \(x=2\) thì \(y=5\) nên đồ thị đi qua hai điểm \(A(0;5)\) và \(B(1;5)\).

Hàm số là hàm số chẵn vì TXĐ: D=R và \(f\left( { - x} \right) = 5 = f\left( x \right)\)

Loigiaihay.com