Bài 1.18 trang 21 SBT hình học 10

Đề bài

Cho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có điểm đặt \( O \) và tạo với nhau góc \({60^0}\). Tìm cường độ tổng hợp lực của hai lực ấy biết rằng cường độ của hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) đều là \(100N\).

Lời giải chi tiết

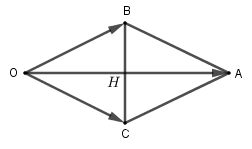
Cố định điểm O, dựng véc tơ \(\overrightarrow {OB}  = \overrightarrow {{F_1}} ,\overrightarrow {OC}  = \overrightarrow {{F_2}} \).

Dựng hình bình hành \(OBAC\) ta có:

\(\overrightarrow {{F_1}}  + \overrightarrow {{F_2}}  = \overrightarrow {OB}  + \overrightarrow {OC}  = \overrightarrow {OA} \) \( \Rightarrow \left| {\overrightarrow {{F_1}}  + \overrightarrow {{F_2}} } \right| = OA\).

Xét hình bình hành \(OBAC\) có \(OB = OC = 100\) nên là hình thoi.

\( \Rightarrow OA \bot BC\) tại \(H\).

Mà \(\widehat {BOC} = {60^0}\) nên tam giác \(BOC\) đều.

Do đó BC=100 và \(BH = \frac{1}{2}BC = 50\)

Theo pitago \(OH = \sqrt {O{B^2} - B{H^2}} \) \( = \sqrt {{{100}^2} - {{50}^2}}  = 50\sqrt 3 \).

Vậy cường độ của hợp lực là \(OA = 2OH = 100\sqrt 3 N\).

Loigiaihay.com