Bài 1.15 trang 21 SBT hình học 10Giải bài 1.15 trang 21 sách bài tập hình học 10. Cho tam giác ABC... Quảng cáo
Đề bài Cho tam giác \(ABC\). Chứng minh rằng nếu \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) thì tam giác \(ABC\) là tam giác vuông tại \(C\). Phương pháp giải - Xem chi tiết - Dựng hình bình hành \(CADB\). - Sử dụng quy tắc hình bình hành và quy tắc trừ véc tơ để nhận xét độ dài các véc tơ. Lời giải chi tiết
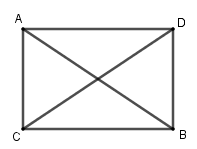
Vẽ hình bình hành \(CADB\). Ta có \(\overrightarrow {CA} + \overrightarrow {CB} = \overrightarrow {CD} \), do đó \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = CD\) Vì \(\overrightarrow {CA} - \overrightarrow {CB} = \overrightarrow {BA} \), Do đó \(\left| {\overrightarrow {CA} - \overrightarrow {CB} } \right| = BA\). Từ \(\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right| = \left| {\overrightarrow {CA} - \overrightarrow {CB} } \right|\) suy ra \(CD = AB\) Vậy tứ giác \(CADB\) là hình chữ nhật. Ta có tam giác \(ABC\) vuông tại \(C\). Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
