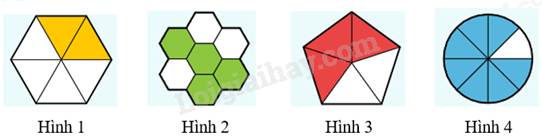
Đề kiểm tra học kì 2 Toán 4 Kết nối tri thức - Đề số 3Đã tô màu (frac{4}{7}) hình nào dưới đây?... Có hai xe chở (frac{7}{4}) tấn hoa quả đến các siêu thị. Xe thứ nhất chở nhiều hơn xe thứ hai (frac{3}{8}) tấn. Vậy khối lượng hoa quả xe thứ hai chở là:...Đề bài
I. Trắc nghiệm
Khoanh vào chữ đặt trước câu trả lời đúng
Câu 2 :
Có hai xe chở \(\frac{7}{4}\) tấn hoa quả đến các siêu thị. Xe thứ nhất chở nhiều hơn xe thứ hai \(\frac{3}{8}\) tấn. Vậy khối lượng hoa quả xe thứ hai chở là:
Câu 3 :
Điền số còn thiếu vào chỗ chấm: \(\frac{3}{7}\)+ .?. = \(\frac{9}{8}\)
Câu 4 :
Mỗi bao xi măng cân nặng 50 kg. Hỏi cần bao nhiêu bao xi măng như thế để có 4 tấn xi măng?
Câu 5 :
Một cửa hàng nhập về 8 tạ gạo. Hôm qua cửa hàng bán được \(\frac{2}{5}\) số gạo nhập về. Hôm nay bán được \(\frac{3}{{10}}\) số gạo nhập về. Vậy trung bình mỗi ngày cửa hàng bán được số ki-lô-gam gạo là:
Câu 6 :
Giá trị của biểu thức 136 x 11 – 11 x 36 là:
II. Tự luận
Lời giải và đáp án
I. Trắc nghiệm
Khoanh vào chữ đặt trước câu trả lời đúng
Đáp án : B Phương pháp giải :
Dựa vào kiến thức về phân số. Lời giải chi tiết :
Hình ảnh biểu thị phân số \(\frac{4}{7}\) là B. Đáp án B.
Câu 2 :
Có hai xe chở \(\frac{7}{4}\) tấn hoa quả đến các siêu thị. Xe thứ nhất chở nhiều hơn xe thứ hai \(\frac{3}{8}\) tấn. Vậy khối lượng hoa quả xe thứ hai chở là:
Đáp án : A Phương pháp giải :
Số bé = (tổng – hiệu) : 2 Lời giải chi tiết :
Khối lượng hoa quả xe thứ hai chở là: \(\left( {\frac{7}{4} - \frac{3}{8}} \right):2 = \frac{{11}}{{16}}\) (tấn) Đáp án A.
Câu 3 :
Điền số còn thiếu vào chỗ chấm: \(\frac{3}{7}\)+ .?. = \(\frac{9}{8}\)
Đáp án : C Phương pháp giải :
Số hạng = Tổng – Số hạng Lời giải chi tiết :
\(\frac{3}{7}\)+ .?. = \(\frac{9}{8}\) ? = \(\frac{9}{8}\) - \(\frac{3}{7}\)= \(\frac{{39}}{{56}}\) Đáp án C.
Câu 4 :
Mỗi bao xi măng cân nặng 50 kg. Hỏi cần bao nhiêu bao xi măng như thế để có 4 tấn xi măng?
Đáp án : D Phương pháp giải :
Đổi 4 tấn ra đơn vị kg Số bao xi măng để có 4 tấn xi măng = Tổng khối lượng xi măng : Khối lượng 1 bao xi măng Lời giải chi tiết :
Đổi 4 tấn = 4 000 kg Cần số bao xi măng như thế để có 4 tấn xi măng là: 4 000 : 50 = 80 bao Đáp án D.
Câu 5 :
Một cửa hàng nhập về 8 tạ gạo. Hôm qua cửa hàng bán được \(\frac{2}{5}\) số gạo nhập về. Hôm nay bán được \(\frac{3}{{10}}\) số gạo nhập về. Vậy trung bình mỗi ngày cửa hàng bán được số ki-lô-gam gạo là:
Đáp án : B Phương pháp giải :
- Đổi: 8 tạ = 800 kg - Tìm số kg gạo hôm qua bán được = số kg gạo nhập về x \(\frac{2}{5}\) - Tìm số kg gạo hôm nay bán được = số kg gạo nhập về x \(\frac{3}{{10}}\) - Tìm số kg gạo trung bình mỗi ngày cửa hàng bán được Lời giải chi tiết :
Đổi: 8 tạ = 800 kg Số kg gạo hôm qua bán được là: \(800 \times \frac{2}{5} = 320\) (kg) Số kg gạo hôm nay bán được là: \(800 \times \frac{3}{{10}} = 240\) (kg) Trung bình mỗi ngày cửa hàng bán được số ki-lô-gam gạo là: (320 + 240) : 2 = 280 (kg) Đáp án B.
Câu 6 :
Giá trị của biểu thức 136 x 11 – 11 x 36 là:
Đáp án : D Phương pháp giải :
- Áp dụng cộng thức: a x b - a x c = a x (b - c) Lời giải chi tiết :
11 x (136 – 36) = 11 x 100 = 1 100 Đáp án D.
II. Tự luận
Phương pháp giải :
- Đặt tính - Với phép nhân: Thực hiện lần lượt từ phải sang trái - Với phép chia: Chia lần lượt từ trái sang phải Lời giải chi tiết :
a)
b)
Phương pháp giải :
Dựa vào cách tìm thành phần chưa biết của phép tính Lời giải chi tiết :
a) ? - \(\frac{5}{{14}} = \frac{3}{7}\) ? = \(\frac{3}{7} + \frac{5}{{14}}\) ? = \(\frac{{11}}{{14}}\) b) \(\frac{2}{{11}}\) x ? \( = \frac{4}{5}\) ? = \(\frac{4}{5}:\frac{2}{{11}}\) ? = \(\frac{4}{5} \times \frac{{11}}{2}\) ? =\(\frac{{22}}{5}\) Phương pháp giải :
a) Sắp xếp các phân số theo thứ tự từ bé đến lớn b) Sắp xếp các phân số theo thứ tự từ lớn đến bé Lời giải chi tiết :
a) Ta có: +) Các phân số bé hơn 1: \(\frac{{132}}{{143}};\frac{{12}}{{17}}\) Ta so sánh \(\frac{{132}}{{143}} và \frac{{12}}{{17}}\) \(\frac{{132}}{{143}} = \frac{{12}}{{13}};\frac{{12}}{{17}}\) là 2 phân số có tử số giống nhau (đều là 12); có mẫu số (13<17) nên \(\frac{{12}}{{17}} < \frac{{12}}{{13}}\)hay \(\frac{{12}}{{17}} < \frac{{132}}{{143}}\) +) \(\frac{7}{7} = 1\) +) Các phân số lớn hơn 1: \(\frac{5}{2};\frac{{21}}{{18}}\) \(\frac{5}{2};\frac{{27}}{{18}} = \frac{3}{2}\) là 2 phân số có mẫu số giống nhau (đều là 2); có tử số (5>3) nên\(\frac{{27}}{{18}} < \frac{5}{2}\) Vậy sắp xếp các phân số theo thứ tự từ bé đến lớn là: \(\frac{{12}}{{17}};\frac{{132}}{{143}};\frac{7}{7};\frac{{21}}{{18}};\frac{5}{2}\) Đáp án: \(\frac{{12}}{{17}};\frac{{132}}{{143}};\frac{7}{7};\frac{{21}}{{18}};\frac{5}{2}\) b) Ta có: \(\frac{1}{2} = \frac{7}{{14}};\frac{1}{7} = \frac{2}{{14}}\) Sắp xếp các phân số theo thứ tự từ lớn đến bé là: \(\frac{9}{{14}};\frac{1}{2};\frac{5}{{14}};\frac{1}{7}\) Đáp án:\(\frac{9}{{14}};\frac{1}{2};\frac{5}{{14}};\frac{1}{7}\) Phương pháp giải :
- Tính tổng số tuổi của bố và mẹ = Trung bình cộng số tuổi của bố và mẹ x 2 - Tính tổng số tuổi của bố, mẹ và Lan = Trung bình cộng số tuổi của bố, mẹ và Lan x 3 - Tính số tuổi của Lan = Tổng số tuổi của bố, mẹ và Lan - Tổng số tuổi của bố và mẹ Lời giải chi tiết :
Tổng số tuổi của bố và mẹ là: 39 x 2 = 78 (tuổi) Tổng số tuổi của bố, mẹ và Lan là: 30 x 3 = 90 (tuổi) Số tuổi của Lan là: 90 – 78 = 12 (tuổi) Đáp số: 12 tuổi Phương pháp giải :
- Áp dụng tính chất giao hoán, kết hợp của phép cộng - Tính bằng cách thuận tiện với phép nhân phân số Lời giải chi tiết :
a) \(\begin{array}{l}\frac{8}{5} + \frac{3}{6} + 2 + \frac{4}{5} + \frac{3}{2} + \frac{3}{5}\\ = (\frac{8}{5} + \frac{4}{5} + \frac{3}{5}) + (\frac{1}{2} + \frac{3}{2}) + 2\\ = \frac{{15}}{5} + \frac{4}{2} + 2\\ = 3 + 2 + 2\\ = 7\end{array}\) b) \((1 - \frac{1}{2})\)×\((1 - \frac{1}{3})\)×\((1 - \frac{1}{5})\) \(\begin{array}{l} = \frac{1}{2} \times \frac{2}{3} \times \frac{3}{4} \times \frac{4}{5}\\ = \frac{1}{5}\end{array}\)
|
























Danh sách bình luận