Lý thuyết Tập hợp và các phép toán trên tập hợp1. Các khái niệm cơ bản về tập hợp Quảng cáo
1. Các khái niệm cơ bản về tập hợp a. Tập hợp + Mô tả tập hợp: Cách 1. Liệt kê các phần tử của tập hợp; Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp. + Quan hệ giữa phần tử và tập hợp: Phần tử a thuộc tập hợp S hay tập hợp S chứa điểm a: \(a \in S\). Phần tử a không thuộc tập hợp S hay tập hợp S không chứa điểm a: \(a \notin S\). + Số phần tử của tập hợp S: \(n(S)\). \(n(S) = 0 \Leftrightarrow S = \emptyset \) (S là tập rỗng). b. Tập hợp con Cho hai tập hợp T và S bất kì. + T là tập hợp con của S nếu Kí hiệu: \(T \subset S\) (T là tập hợp con của S) hoặc \(S \supset T\) (S chứa T hoặc T chứa trong S). Số tập hợp con của tập S có n phần tử là: \({2^n}\). + T không là tập con của S nếu Kí hiệu: \(T \not\subset S\). Quy ước: \(\emptyset \) và T là tập con của tập hợp T. c. Hai tập hợp bằng nhau \(S = T\) nếu \(S \subset T\) và \(T \subset S\).
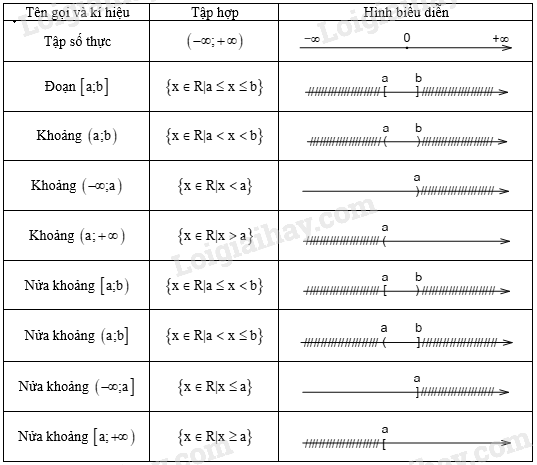
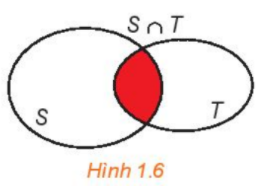
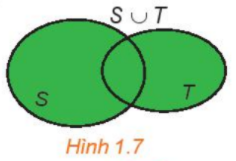
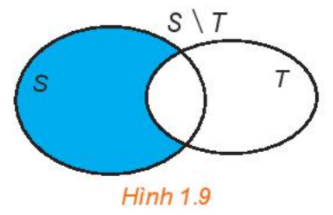
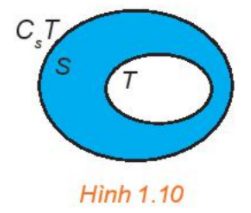
2. Các tập hợp số a. Mối quan hệ giữa các tập hợp số Tập hợp các số tự nhiên \(\mathbb{N} = \{ 0;1;2;3;4;5;...\} \) (\(\mathbb{N}^* = \mathbb{N}{\rm{\backslash }}\{ 0\} \)). Tập hợp các số nguyên \(\mathbb{Z} = \{ ...; - 3; - 2; - 1;0;1;2;3;...\} \): gồm các số nguyên âm và các số tự nhiên. Tập hợp các số hữu tỉ \(\mathbb{Q} = \left\{ {\frac{a}{b}|a,b \in \mathbb{Z};b \ne 0} \right\}\): gồm các số nguyên và các số thập phân hữu hạn hoặc vô hạn tuần hoàn. Tập hợp các số thực \(\mathbb{R}\): gồm các số hữu tỉ và các số vô tỉ. (Số vô tỉ là các số thập phân vô hạn không tuần hoàn). Mối quan hệ giữa các tập hợp số: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\) b. Các tập con thường dùng của \(\mathbb{R}\) 3. Các phép toán trên tập hợp a. Giao của hai tập hợp Giao của hai tập hợp S và T (kí hiệu \(S \cap T\)) là tập hợp gồm các phần tử thuộc cả hai tập hợp S và T. \(S \cap T = \{ x|x \in S\) và \(x \in T\} .\) b. Hợp của hai tập hợp Hợp của hai tập hợp S và T (kí hiệu \(S \cup T\)) là tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp T. \(S \cup T = \{ x|x \in S\) hoặc \(x \in T\} \). c. Hiệu của hai tập hợp Hiệu của hai tập hợp S và T (kí hiệu \(S{\rm{\backslash }}T\)) là tập hợp gồm các phần tử thuộc S nhưng không thuộc T. \(S{\rm{\backslash }}T = \{ x|x \in S\) và \(x \notin T\} \). Nếu \(T \subset S\) thì \(S{\rm{\backslash }}T\) được gọi là phần bù của T trong S, kí hiệu là \({C_S}T.\) Ví dụ: \({C_\mathbb{Z}}\mathbb{N} = \mathbb{Z}{\rm{\backslash }}\mathbb{N} = \{ x|x \in \mathbb{Z}\) và \(x \notin \mathbb{N}\} = \{ ...; - 3; - 2; - 1\} \). Đặc biệt: \({C_S}S = \emptyset \).
|





















Danh sách bình luận