Lý thuyết Giải hệ hai phương trình bậc nhất hai ẩn Toán 9 Kết nối tri thức1. Cách giải hệ phương trình bằng phương pháp thế Quảng cáo
1. Cách giải hệ phương trình bằng phương pháp thế
Lưu ý: Tùy theo hệ phương trình, ta có thể lựa chọn cách biểu diễn x theo y hoặc y theo x. Ví dụ: 1. Hệ phương trình \(\left\{ \begin{array}{l}2x - y = 3\\x + 2y = 4\end{array} \right.\) được giải bằng phương pháp thế như sau: Từ phương trình thứ nhất của hệ, ta có \(y = 2x - 3\). Thế vào phương trình thứ hai của hệ, ta được \(x + 2\left( {2x - 3} \right) = 4\) hay \(5x - 6 = 4\), suy ra \(x = 2\). Từ đó \(y = 2.2 - 3 = 1\). Vậy hệ phương trình đã cho có nghiệm là \(\left( {2;1} \right)\). 2. Hệ phương trình \(\left\{ \begin{array}{l}x - y = - 2\\2x - 2y = 8\end{array} \right.\) được giải bằng phương pháp thế như sau: Từ phương trình thứ nhất của hệ, ta có \(x = y - 2\). Thế vào phương trình thứ hai của hệ, ta được \(2\left( {y - 2} \right) - 2y = 8\) hay \(0y - 4 = 8\). Do không có giá trị vào của y thỏa mãn hệ thức \(0y - 4 = 8\) nên hệ phương trình vô nghiệm. 3. Hệ phương trình \(\left\{ \begin{array}{l} - x + y = - 2\\3x - 3y = 6\end{array} \right.\) được giải bằng phương pháp thế như sau: Từ phương trình thứ nhất của hệ, ta có \(y = x - 2\). Thế vào phương trình thứ hai của hệ, ta được \(3x - 3\left( {x - 2} \right) = 6\) hay \(0x = 0\). Ta thấy mọi giá trị của x đều thỏa mãn \(0x = 0\). Với giá trị tùy ý của x, giá trị tương ứng của y được tính bởi \(y = x - 2\). Vậy hệ phương trình có nghiệm là \(\left( {x;x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý. 2. Cách giải hệ phương trình bằng phương pháp cộng đại số:
Ví dụ: 1. Hệ phương trình \(\left\{ \begin{array}{l}5x - 7y = 9\\5x - 3y = 1\end{array} \right.\) được giải bằng phương pháp cộng đại số như sau: Trừ từng vế hai phương trình ta được \(\left( {5x - 5x} \right) + \left( { - 7y + 3y} \right) = 9 - 1\) hay \( - 4y = 8\), suy ra \(y = - 2\). Thế \(y = - 2\) vào phương trình thứ hai ta được \(5x - 7.\left( { - 2} \right) = 9\) hay \(5x + 14 = 9\), suy ra \(x = - 1\). Vậy hệ phương trình đã cho có nghiệm là (-1;-2). 2. Hệ phương trình \(\left\{ \begin{array}{l}3x - 5y = 2\\ - 6x + 10y = - 4\end{array} \right.\) được giải bằng phương pháp cộng đại số như sau: Chia hai vế của phương trình thứ hai cho 2, ta được hệ \(\left\{ \begin{array}{l}3x - 5y = 2\\ - 3x + 5y = - 2\end{array} \right.\) Cộng từng vế hai phương trình của hệ mới ta có \(0x + 0y = 0\). Hệ này luôn thỏa mãn với các giá trị tùy ý của x và y. Với giá trị tùy ý của x, giá trị của y được tính nhờ hệ thức \(3x - 5y = 2\), suy ra \(y = \frac{3}{5}x - \frac{2}{5}\). Vậy hệ phương trình đã cho cho nghiệm là \(\left( {x;\frac{3}{5}x - \frac{2}{5}} \right)\) với \(x \in \mathbb{R}\). 3. Cách tìm nghiệm của hệ hai phương trình bằng máy tính cầm tay
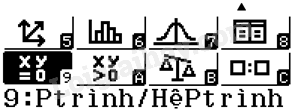
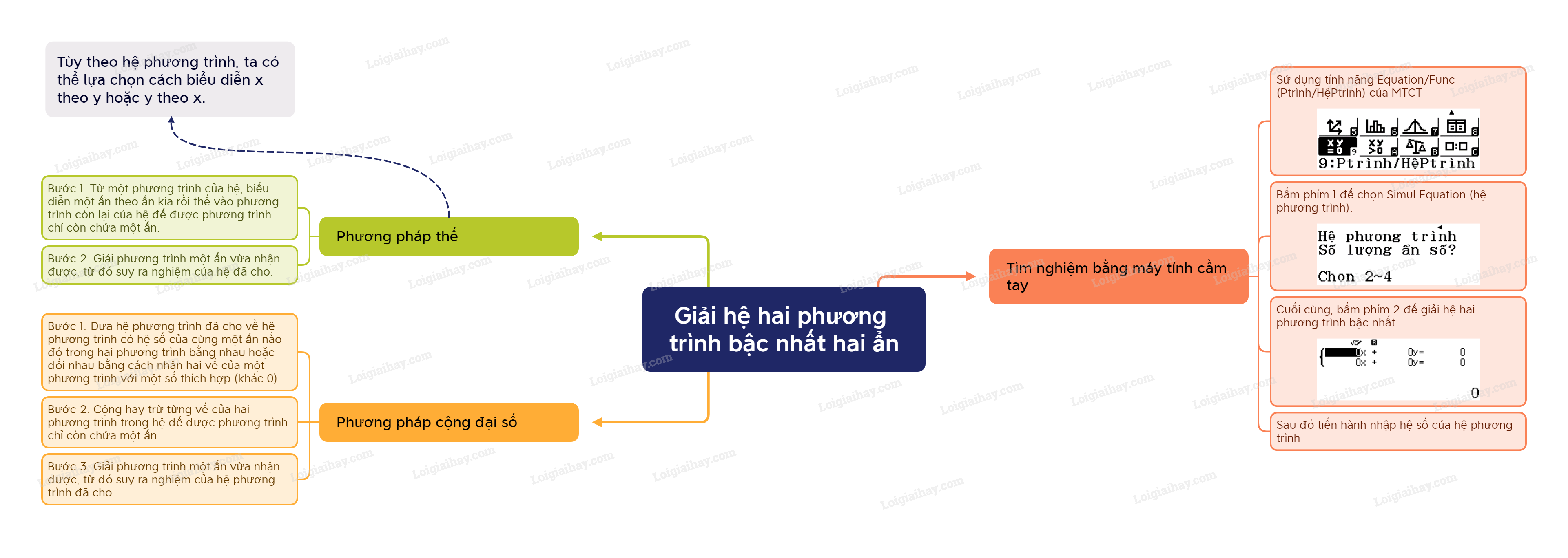
Ví dụ: Giải hệ \(\left\{ \begin{array}{l}2x + y - 4 = 0\\ - 2x + y = 0\end{array} \right.\), ta viết nó dưới dạng \(\left\{ \begin{array}{l}2x + y = 4\\ - 2x + y = 0\end{array} \right.\). Khi đó, ta có \({a_1} = 2\), \({b_1} = 1\), \({c_1} = 4\), \({a_2} = - 2\), \({b_2} = 1\), \({c_2} = 0\). Lần lượt thực hiện các bước sau: Bước 1. Vào chức năng hệ hai phương trình bậc nhất hai ẩn bằng cách nhấn MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).
Bấm phím 1 để chọn Simul Equation (hệ phương trình).
Cuối cùng, bấm phím 2 để giải hệ hai phương trình bậc nhất
Bước 2. Ta nhập các hệ số \({a_1},{b_1},{c_1},{a_2},{b_2},{c_2}\) bằng cách bấm
Bước 3. Sau khi nhập xong, ta bấm phím =, màn hình hiện x = 1; tiếp tục bấm =, màn hình hiện y = 2. Ta hiểu nghiệm của hệ phương trình là (1;2). Chú ý: - Muốn xóa số vừa mới nhập thì bấm phím AC, muốn thay đổi số đã nhập ở vị trí nào đó thì di chuyển con trỏ đến vị trí đó rồi nhập số mới. - Bấm phím ▲ hay ▼ để chuyển hiển thị các giá trị của x và y trong kết quả. - Nếu máy báo Infinite Solution thì hệ phương trình đã cho có vô số nghiệm. Nếu máy báo No Solution thì hệ phương trình đã cho vô nghiệm.
|























Danh sách bình luận