Lý thuyết Các khái niệm mở đầu

1. KHÁI NIỆM VECTƠ

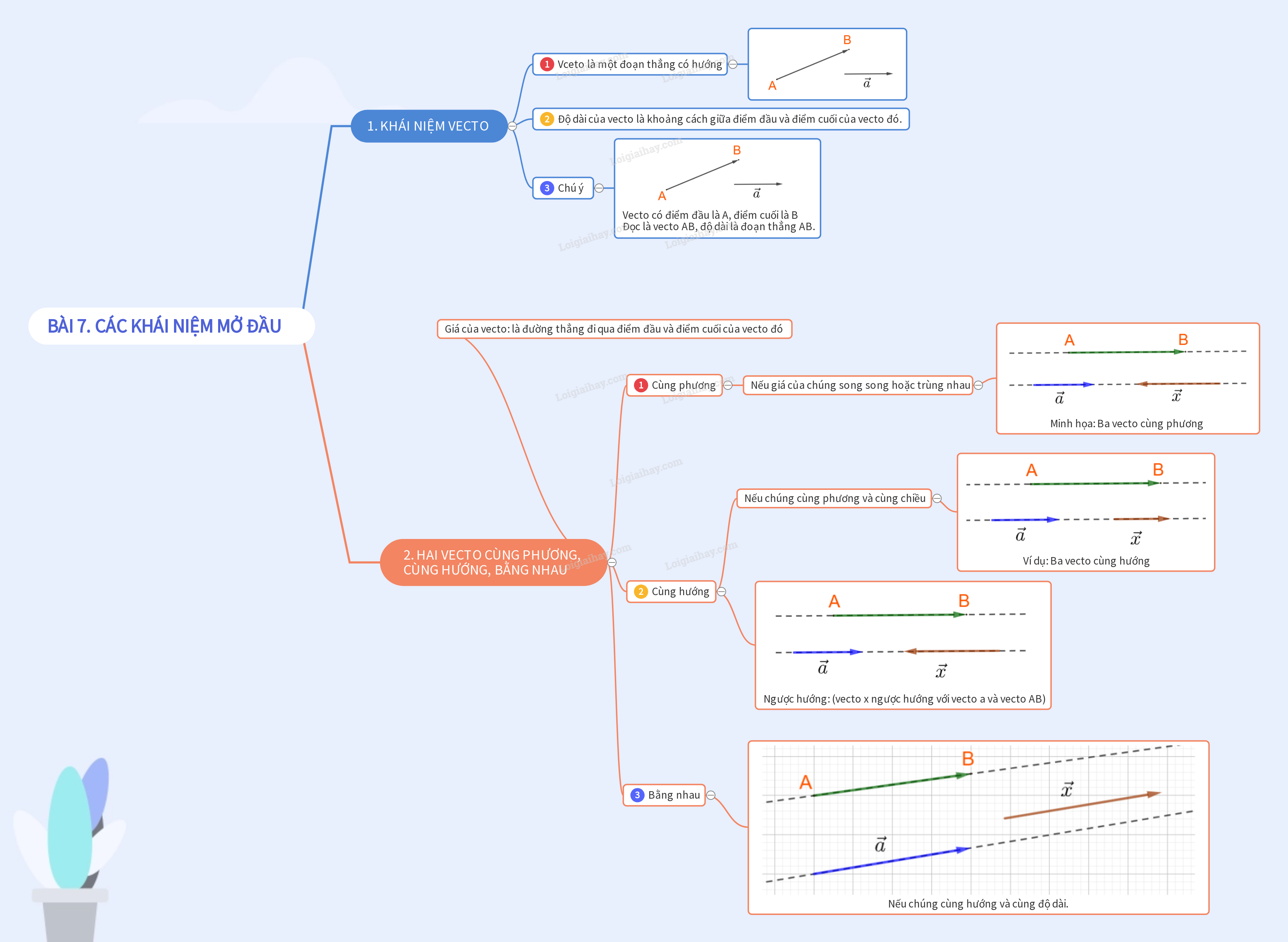
+) Vecto là một đoạn thẳng có hướng.

Ví dụ 1: i) vecto \(\overrightarrow {AB} \): (đọc là vecto AB)   

ii) Vecto \(\overrightarrow {BA} \): 

iii) vecto \(\overrightarrow u \): 

+) Độ dài của vecto là khoảng cách giữa điểm đầu và điểm cuối của vecto đó.

Kí hiệu: độ dài của vecto \(\overrightarrow {AB} \) là \(\left| {\overrightarrow {AB} } \right|\).

Ví dụ 2: \(\left| {\overrightarrow {AB} } \right| = AB;\;\left| {\overrightarrow {DE} } \right| = DE\)

+) Vecto không, là vecto có độ dài bằng 0. Ví dụ: \(\overrightarrow {AA} ,\;\overrightarrow {EE} ,...\)(điểm đầu trùng điểm cuối)

Kí hiệu chung là \(\overrightarrow 0 \).

2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU

+) Giá của vecto:  là đường thẳng đi qua điểm đầu và điểm cuối của vecto đó.

Ví dụ: Giá của vecto \(\overrightarrow {CD} \) là đường thẳng CD

+) Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

+) Hai vecto cùng phương thì chúng cùng hướng hoặc ngược hướng.

Ví dụ:

Ba vecto \(\overrightarrow u ,\;\overrightarrow {CD} ,\;\overrightarrow {AB} \) cùng phương.

Trong đó 2 vecto \(\overrightarrow u ,\;\overrightarrow {CD} \) cùng hướng, còn 2 vecto \(\overrightarrow {CD} ,\;\overrightarrow {AB} \) ngược hướng.

+) Hai vecto được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.

* Chú ý:

- Chỉ khi hai vecto cùng phương ta mới nói tới chúng cùng hướng hay ngược hướng.

- Vecto \(\overrightarrow 0 \) cùng phương, cùng hướng với mọi vecto.

- Với mỗi điểm O và vecto \(\overrightarrow a \) cho trước, có duy nhất điểm A sao cho \(\overrightarrow {OA}  = \overrightarrow a \)

* Nhận xét:

+) Ba điểm A, B, C thẳng hàng khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương.

+) Ba điểm A, B, C thẳng hàng, B nằm giữa khi và chỉ khi \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng hướng.