Giải mục 3 trang 35, 36, 37, 38 SGK Toán 12 tập 2 - Chân trời sáng tạo

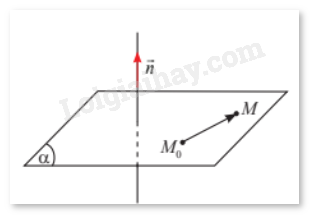
HĐ3

Trả lời câu hỏi Hoạt động 3 trang 35 SGK Toán 12 Chân trời sáng tạo

Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha  \right)\) đi qua điểm \({M_0}\left( {1;2;3} \right)\) và nhận \(\vec n = \left( {7;5;2} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x;y;z} \right)\) là một điểm tuỳ ý trong không gian. Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \) theo \(x,y,z\).

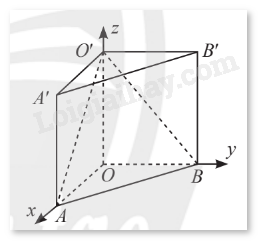
Phương pháp giải:

Tính toạ độ vectơ \(\overrightarrow {{M_0}M} \), sau đó tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \).

Lời giải chi tiết:

Toạ độ của vectơ \(\overrightarrow {{M_0}M} \) là \(\left( {x - 1;y - 2;z - 3} \right)\)

Suy ra \(\vec n.\overrightarrow {{M_0}M}  = 7\left( {x - 1} \right) + 5\left( {y - 2} \right) + 2\left( {z - 3} \right) = 7x + 5y + 2z - 23\)

TH3

Trả lời câu hỏi Thực hành 3 trang 36 SGK Toán 12 Chân trời sáng tạo

Cho hai mặt phẳng \(\left( \alpha  \right)\), \(\left( \beta  \right)\) có phương trình tổng quát là \(\left( \alpha  \right):2x + 2y - 3z - 4 = 0\) và \(\left( \beta  \right):x + 4z - 12 = 0\).

a) Tìm một vectơ pháp tuyến của mỗi mặt phẳng \(\left( \alpha  \right)\), \(\left( \beta  \right)\).

b) Tìm điểm thuộc mặt phẳng \(\left( \alpha  \right)\) trong số các điểm \(M\left( {1;0;1} \right)\), \(N\left( {1;1;0} \right)\).

Phương pháp giải:

a) Một vectơ pháp tuyến của mặt phẳng có phương trình \(Ax + By + Cz + D = 0\) (trong đó \(A\), \(B\), \(C\) không đồng thời bằng 0) là \(\vec n = \left( {A,B,C} \right)\).

b) Điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) nằm trên mặt phẳng \(\left( \alpha  \right):Ax + By + Cz + D = 0\) khi và chỉ khi \(A{x_0} + B{y_0} + C{z_0} + D = 0\)

Lời giải chi tiết:

a) Phương trình mặt phẳng \(\left( \alpha  \right)\) là \(2x + 2y - 3z - 4 = 0\) nên \(\left( \alpha  \right)\) nhận \(\overrightarrow {{n_{\left( \alpha  \right)}}}  = \left( {2;2; - 3} \right)\) làm một vectơ pháp tuyến.

Phương trình mặt phẳng \(\left( \beta  \right)\) là \(x + 4z - 12 = 0\) nên \(\left( \beta  \right)\) nhận \(\overrightarrow {{n_{\left( \beta  \right)}}}  = \left( {1;0;4} \right)\) làm một vectơ pháp tuyến.

b) Thay điểm \(M\left( {1;0;1} \right)\) vào phương trình mặt phẳng \(\left( \alpha  \right)\), ta được:

\(2.1 + 2.0 - 3.1 - 4 =  - 5 \ne 0\).

Vậy điểm \(M\) không thuộc \(\left( \alpha  \right)\).

Thay điểm \(N\left( {1;1;0} \right)\) vào phương trình mặt phẳng \(\left( \alpha  \right)\), ta được:

\(2.1 + 2.1 - 3.0 - 4 = 0\).

Vậy điểm \(N\) thuộc \(\left( \alpha  \right)\).

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 36 SGK Toán 12 Chân trời sáng tạo

Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha  \right)\) đi qua điểm \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A,B,C} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x,y,z} \right)\) là một điểm tuỳ ý trong không gian.

a) Tìm toạ độ của \(\overrightarrow {{M_0}M} \).

b) Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \).

c) Lập phương trình tổng quát của mặt phẳng \(\left( \alpha  \right)\).

Phương pháp giải:

a) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right)\)

b) Sử dụng công thức tích vô hướng để tính \(\vec n.\overrightarrow {{M_0}M} \).

c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha  \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha  \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M}  = 0\)

Lời giải chi tiết:

a) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right) = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)

b) Ta có: \(\vec n.\overrightarrow {{M_0}M}  = A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right)\)

c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha  \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha  \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M}  = 0\).

Suy ra \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)

Vậy phương trình mặt phẳng \(\left( \alpha  \right)\) là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 36 SGK Toán 12 Chân trời sáng tạo

Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha  \right)\) đi qua điểm \(M\left( {0,2,1} \right)\) và có cặp vectơ chỉ phương là \(\vec a = \left( {1;3;1} \right)\), \(\vec b = \left( {2;0;1} \right)\)

a) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha  \right)\).

b) Lập phương trình của mặt phẳng \(\left( \alpha  \right)\).

Phương pháp giải:

a) Do \(\left( \alpha  \right)\) nhận \(\vec a\) và \(\vec b\) làm một cặp vectơ chỉ phương, nên \(\left( \alpha  \right)\) sẽ nhận vectơ \(\vec n = \left[ {\vec a,\vec b} \right]\) làm một vectơ pháp tuyến.

b) Phương trình mặt phẳng \(\left( \alpha  \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là .

Lời giải chi tiết:

a) Do \(\left( \alpha  \right)\) nhận \(\vec a\) và \(\vec b\) làm một cặp vectơ chỉ phương, nên \(\left( \alpha  \right)\) sẽ nhận vectơ \(\vec n = \left[ {\vec a,\vec b} \right]\) làm một vectơ pháp tuyến.

Tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) là:

\(\left[ {\vec a,\vec b} \right] = \left( {3.1 - 1.0;1.2 - 1.1;1.0 - 3.2} \right) = \left( {3;1; - 6} \right)\).

Vậy \(\left( \alpha  \right)\) nhận \(\vec n = \left( {3;1; - 6} \right)\) làm một vectơ pháp tuyến.

b) Mặt phẳng \(\left( \alpha  \right)\) đi qua \(M\left( {0,2,1} \right)\) và nhận \(\vec n = \left( {3;1; - 6} \right)\) làm một vectơ pháp tuyến, nên phương trình mặt phẳng \(\left( \alpha  \right)\) là:

\(3\left( {x - 0} \right) + 1\left( {y - 2} \right) - 6\left( {z - 1} \right) = 0 \Leftrightarrow 3x + y - 6z + 4 = 0\).

HĐ6

Trả lời câu hỏi Hoạt động 6 trang 37 SGK Toán 12 Chân trời sáng tạo

Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha  \right)\) đi qua ba điểm \(A\left( {0;1;1} \right)\), \(B\left( {2;4;3} \right)\), \(C\left( {5;3;1} \right)\).

a) Tìm toạ độ một cặp vectơ chỉ phương của mặt phẳng \(\left( \alpha  \right)\).

b) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha  \right)\).

c) Lập phương trình của mặt phẳng \(\left( \alpha  \right)\).

Phương pháp giải:

a) Mặt phẳng \(\left( \alpha  \right)\) đi qua ba điểm \(A\), \(B\), \(C\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).

b) Một vectơ pháp tuyến của \(\left( \alpha  \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).

c) Phương trình mặt phẳng \(\left( \alpha  \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

Lời giải chi tiết:

a) Mặt phẳng \(\left( \alpha  \right)\) đi qua ba điểm \(A\left( {0;1;1} \right)\), \(B\left( {2;4;3} \right)\), \(C\left( {5;3;1} \right)\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB}  = \left( {2;3;2} \right)\) và \(\overrightarrow {AC}  = \left( {5;2;0} \right)\).

b) Do \(\left( \alpha  \right)\) có một cặp vectơ chỉ phương là \(\overrightarrow {AB}  = \left( {2;3;2} \right)\) và \(\overrightarrow {AC}  = \left( {5;2;0} \right)\), nên một vectơ pháp tuyến của \(\left( \alpha  \right)\) là:

\(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {3.0 - 2.2;2.5 - 2.0;2.2 - 3.5} \right) = \left( { - 4;10; - 11} \right)\).

c) Mặt phẳng \(\left( \alpha  \right)\) đi qua \(A\left( {0;1;1} \right)\) và có một vectơ pháp tuyến là \(\vec n = \left( { - 4;10; - 11} \right)\) nên phương trình mặt phẳng \(\left( \alpha  \right)\) là:

\( - 4\left( {x - 0} \right) + 10\left( {y - 1} \right) - 11\left( {z - 1} \right) = 0 \Leftrightarrow  - 4x + 10y - 11z + 1 = 0\).

TH4

Trả lời câu hỏi Thực hành 4 trang 38 SGK Toán 12 Chân trời sáng tạo

Viết phương trình mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:

a) \(\left( P \right)\) đi qua điểm \(A\left( {2;0; - 1} \right)\) và có vectơ pháp tuyến \(\vec n = \left( {5; - 2;7} \right)\).

b) \(\left( P \right)\) đi qua điểm \(B\left( { - 2;3;0} \right)\) và có cặp vectơ chỉ phương là \(\vec u = \left( {2;2; - 1} \right)\), \(\vec v = \left( {3;1;0} \right)\).

c) \(\left( P \right)\) đi qua ba điểm \(A\left( {2;1;5} \right)\), \(B\left( {3;2;7} \right)\), \(C\left( {4;1;6} \right)\).

d) \(\left( P \right)\) đi qua ba điểm \(M\left( {7;0;0} \right)\), \(N\left( {0; - 2;0} \right)\), \(P\left( {0;0;9} \right)\).

Phương pháp giải:

a) Phương trình mặt phẳng \(\left( P \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).

b) Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left[ {\vec u,\vec v} \right]\). Sau đó viết phương trình mặt phẳng \(\left( P \right)\) khi biết một điểm đi qua và một vectơ pháp tuyến.

c) Xác định một cặp vectơ chỉ phương, từ đó tính tích có hướng của cặp vectơ chỉ phương đó để tìm một vectơ pháp tuyến của \(\left( P \right)\). Sau đó viết phương trình mặt phẳng \(\left( P \right)\) khi biết một điểm đi qua và một vectơ pháp tuyến.

d) Sử dụng phương trình mặt phẳng theo đoạn chắn.

Lời giải chi tiết:

a) Mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {2;0; - 1} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {5; - 2;7} \right)\) nên có phương trình là \(5\left( {x - 2} \right) - 2\left( {y - 0} \right) + 7\left( {z + 1} \right) = 0 \Leftrightarrow 5x - 2y + 7z - 3 = 0\).

b) Một vectơ pháp tuyến của \(\left( P \right)\) là:

\(\vec n = \left[ {\vec u,\vec v} \right] = \left( {2.0 - \left( { - 1} \right).1; - 1.3 - 2.0;2.1 - 2.3} \right) = \left( {1; - 3; - 4} \right)\).

Mặt phẳng \(\left( P \right)\) đi qua \(B\left( { - 2;3;0} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {1; - 3; - 4} \right)\) nên có phương trình là \(1\left( {x + 2} \right) - 3\left( {y - 3} \right) - 4\left( {z - 0} \right) = 0 \Leftrightarrow x - 3y - 4z + 11 = 0\).

c) Mặt phẳng \(\left( P \right)\) đi qua ba điểm \(A\left( {2;1;5} \right)\), \(B\left( {3;2;7} \right)\), \(C\left( {4;1;6} \right)\) nên có 1 cặp vectơ chỉ phương là \(\overrightarrow {AB}  = \left( {1;1;2} \right)\) và \(\overrightarrow {AC}  = \left( {2;0;1} \right)\). Do đó một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {1.1 - 2.0;2.2 - 1.1;1.0 - 1.2} \right) = \left( {1;3; - 2} \right)\).

Mặt phẳng \(\left( P \right)\) đi qua \(A\left( {2;1;5} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {1;3; - 2} \right)\) nên có phương trình là \(1\left( {x - 2} \right) + 3\left( {y - 1} \right) - 2\left( {z - 5} \right) = 0 \Leftrightarrow x + 3y - 2z + 5 = 0\).

d) Mặt phẳng \(\left( P \right)\) đi qua ba điểm \(M\left( {7;0;0} \right)\), \(N\left( {0; - 2;0} \right)\), \(P\left( {0;0;9} \right)\) nên phương trình mặt phẳng \(\left( P \right)\) là \(\frac{x}{7} + \frac{y}{{ - 2}} + \frac{z}{9} = 1\).

VD3

Trả lời câu hỏi Vận dụng 3 trang 38 SGK Toán 12 Chân trời sáng tạo

Trong không gian \(Oxyz\), cho hình lăng trụ \(OAB.O'A'B'\). Biết \(O\) là gốc toạ độ, \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\), \(O'\left( {0;0;5} \right)\). Viết phương trình các mặt phẳng \(\left( {O'AB} \right)\) và \(\left( {O'A'B'} \right)\).

Phương pháp giải:

Viết phương trình mặt phẳng \(\left( {O'AB} \right)\) dưới dạng phương trình mặt phẳng theo đoạn chắn. Viết phương trình mặt phẳng \(\left( {O'A'B'} \right)\) do nó đi qua điểm \(O'\) và có một vectơ pháp tuyến \(OO'\).

Lời giải chi tiết:

Mặt phẳng \(\left( {O'AB} \right)\) đi qua \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\), \(O'\left( {0;0;5} \right)\) nên phương trình mặt phẳng \(\left( {O'AB} \right)\) là \(\frac{x}{2} + \frac{y}{3} + \frac{z}{5} = 1\).

Theo hình vẽ, hình lăng trụ \(OAB.O'A'B'\) có các cạnh bên vuông góc với đáy, nên ta có \(OO' \bot \left( {O'A'B'} \right)\). Suy ra \[\overrightarrow {OO'}  = \left( {0;0;5} \right)\] là một vectơ pháp tuyến của mặt phẳng \(\left( {O'A'B'} \right)\).

Hơn nữa, mặt phẳng \(\left( {O'A'B'} \right)\) đi qua \(O'\left( {0;0;5} \right)\) nên phương trình mặt phẳng \(\left( {O'A'B'} \right)\) là \(0\left( {x - 0} \right) + 0\left( {y - 0} \right) + 5\left( {z - 5} \right) = 0 \Leftrightarrow z - 5 = 0\).