Giải mục 1 trang 34, 35 SGK Toán 10 tập 1 - Kết nối tri thứca) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau: Tìm các giá trị lượng giác của góc 120 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
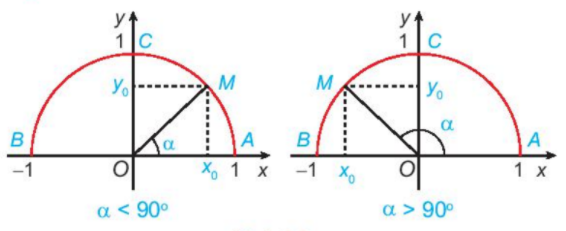
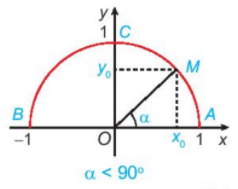
HĐ1 Trả lời câu hỏi Hoạt động 1 trang 34 SGK Toán 10 Kết nối tri thức a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau: \(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\) b) Khi \({0^o} < \alpha < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.
Phương pháp giải: a) Quan sát góc \(\alpha = \widehat {xOM}\) trong các trường hợp tương ứng. Khi ấy M thuộc cung nào? b) Khi \({0^o} < \alpha < {90^o}\) thì \(\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}},\;\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}};\) trong đó \(OM = R = 1\). Lời giải chi tiết: a) Khi \(\alpha = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\)) Khi \(\alpha < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung); Khi \(\alpha > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung). b) Khi \({0^o} < \alpha < {90^o}\) , ta có:
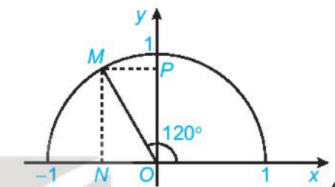
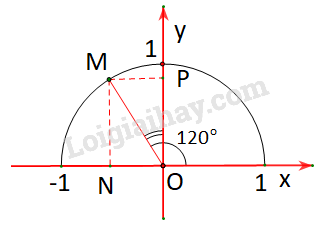
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\). Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\). Vậy \(\cos \alpha \) là hoành độ \({x_0}\) của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M. LT1 Trả lời câu hỏi Luyện tập 1 trang 35 SGK Toán 10 Kết nối tri thức Tìm các giá trị lượng giác của góc \({120^o}\) (H.3.4).
Phương pháp giải: Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\). Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {120^o},\;\sin {120^o}\). Từ đó suy ra \(\tan {120^o} = \dfrac{{\sin {{120}^o}}}{{\cos {{120}^o}}},\;\cot {120^o} = \dfrac{{\cos {{120}^o}}}{{\sin {{120}^o}}}.\) Lời giải chi tiết: Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\) Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Vì \(\widehat {xOM} = {120^o} > {90^o}\) nên M nằm bên trái trục tung. Khi đó: \(\cos {120^o} = -{ON} ,\;\sin {120^o} = {OP} \). Vì \(\widehat {xOM} = {120^o}\) nên \(\widehat {NOM} = {180^o} - {120^o} = {60^o}\) và \(\widehat {POM} = {120^o} - {90^o} = {30^o}\). Vậy các tam giác \(\Delta MON\) và \(\Delta MOP\) vuông tại N, p và có một góc bằng \({30^o}\) \( \Rightarrow ON = MP = \frac{1}{2}OM = \frac{1}{2}\) (trong tam giác vuông, cạnh đối diện góc \({30^o}\) bằng một nửa cạnh huyền). Và \(OP = MN = \sqrt {O{M^2} - O{N^2}} \) \(= \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\). Vậy điểm M có tọa độ là \(\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\). Và \(\cos {120^o} = - \frac{1}{2};\;\sin {120^o} = \frac{{\sqrt 3 }}{2}\). \(\begin{array}{l} \Rightarrow \tan {120^o} = \frac{{\sin {{120}^o}}}{{\cos {{120}^o}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 ;\\\cot {120^o} = \frac{{\cos {{120}^o}}}{{\sin {{120}^o}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = \frac{{ - 1}}{{\sqrt 3 }} = - \frac{{\sqrt 3 }}{3}.\end{array}\) Chú ý Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({120^o}\) Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau: Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ) Tính \(\sin {120^o}\), bấm phím: sin 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 3 }}{2}\) Tính \(\cos {120^o}\),bấm phím: cos 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{ - 1}}{2}\) Tính \(\tan {120^o}\), bấm phím: tan 1 2 0 \(^o\)’’’ = ta được kết quả là \( - \sqrt 3 \) ( Để tính \(\cot {120^o}\), ta tính \(1:\tan {120^o}\))
|




















Danh sách bình luận