Giải câu hỏi trang 114, 115, 116 SGK Toán 9 tập 1 - Kết nối tri thứcTính toán lượng chất tan và dung môi để pha chế dung dịch có nồng độ phần trăm cho trước Ta cần tính số gam đường cát và số gam nước tinh khiết cần thiết để tạo ra n = 1000 (ml) dung dịch có nồng độ a%. Biết rằng khối lượng riêng của đường cát là d = 1,1 (g/ml) và 1 lít nước tinh khiết nặng 1kg. a) Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế. Lập biểu thức tính thể tích và nồng độ dung dịch để chứng minh x, y thỏa mãn hệ phương trình (left{ begin{array}{l}f Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
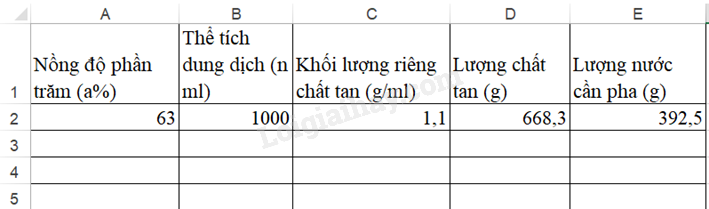
HĐ1 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 1 trang 114 SGK Toán 9 Kết nối tri thức Tính toán lượng chất tan và dung môi để pha chế dung dịch có nồng độ phần trăm cho trước Ta cần tính số gam đường cát và số gam nước tinh khiết cần thiết để tạo ra n = 1000 (ml) dung dịch có nồng độ a%. Biết rằng khối lượng riêng của đường cát là d = 1,1 (g/ml) và 1 lít nước tinh khiết nặng 1kg. a) Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế. Lập biểu thức tính thể tích và nồng độ dung dịch để chứng minh x, y thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}\frac{x}{{1,1}} + y = 1000\\\frac{x}{{x + y}}.100 = a\end{array} \right.\) b) Biến đổi hệ phương trình trên về dạng hệ hai phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}x + 1,1y = 1100\\\left( {100 - a} \right)x - ay = 0\end{array} \right.\) Từ đó chứng tỏ \(\left( {x;y} \right)\) của hệ phương trình này là \(\left\{ \begin{array}{l}x = \frac{{1100a}}{{110 - 0,1a}}\\y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\end{array} \right.\) c) Áp dụng: Tính lượng nước và đường cát tương ứng để pha n = 1000 ml nước đường với nồng độ là a = 63%. Phương pháp giải: Nồng độ phần trăm C của một dung dịch tính bằng công thức \(C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}} \times 100\% \) Trong đó: \({m_{ct}}\) là khối lượng chất tan; \({m_{dd}}\) là khối lượng dung dịch Tính thể tích của một chất = khối lượng của chất đó : khối lượng riêng Lời giải chi tiết: Gọi x (gam) và y (gam) lần lượt là lượng đường cát và nước cất cần pha chế Thể tích của x gam đường cát là \(\frac{x}{{1,1}}\) (ml) Thể tích của y gam nước cất là y (ml) Thể tích của dung dịch gồm x gam đường cát và y gam nước cất là \(\frac{x}{{1,1}} + y = 1000\left( 1 \right)\) (ml) Khối lượng dung dịch là \(x + y\) (gam) Dung dịch có nồng độ a% nên ta có: \(\frac{x}{{x + y}}.100 = a\left( 2 \right)\) Từ (1) và (2) ta có x và y là nghiệm của hệ \(\left\{ \begin{array}{l}\frac{x}{{1,1}} + y = 1000\\\frac{x}{{x + y}}.100 = a\end{array} \right.\) b) Nhân cả hai vế của phương trình (1) với 1,1 ta được \(x + 1,1y = 1100\left( 3 \right)\) Từ (2) ta có \(\frac{{100x}}{{x + y}} = a\) hay \(100x = a\left( {x + y} \right)\) nên \(x\left( {100 - a} \right) - ay = 0\left( 4 \right)\) Từ (3) và (4) nên ta có hệ phương trình \(\left\{ \begin{array}{l}x + 1,1y = 1100\\\left( {100 - a} \right)x - ay = 0\end{array} \right.\) Từ phương trình (3) ta có \(x = 1100 - 1,1y\) thay vào phương trình (4) ta được \(\left( {100 - a} \right)\left( {1100 - 1,1y} \right) - ay = 0\) hay \(1100\left( {100 - a} \right) - 1,1y\left( {100 - a} \right) - ay = 0\) suy ra \(y\left( {1,1.\left( {100 - a} \right) + a} \right) = 1100\left( {100 - a} \right)\) nên \(y\left( {110 - 0,1a} \right) = 1100\left( {100 - a} \right)\) do đó \(y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\) Mà \(x = 1100 - 1,1y = 1100 - 1,1.\frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}} = 1100 - \frac{{1210\left( {100 - a} \right)}}{{110 - 0,1a}}\) \( = \frac{{121000 - 110a - 121000 + 1210a}}{{110 - 0,1a}} = \frac{{1100a}}{{110 - 0,1a}}\) Nên \(\left( {x;y} \right)\) của hệ phương trình này là \(\left\{ \begin{array}{l}x = \frac{{1100a}}{{110 - 0,1a}}\\y = \frac{{1100\left( {100 - a} \right)}}{{110 - 0,1a}}\end{array} \right.\) c) Với a = 63% ta có \(\left\{ \begin{array}{l}x = \frac{{1100.63}}{{110 - 0,1.63}}\\y = \frac{{1100\left( {100 - 63} \right)}}{{110 - 0,1.63}}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \approx 668,3\\y \approx 392,5\end{array} \right.\) Vậy cần khoảng 668,3 gam đường cát và 392,5 gam nước cất. HĐ2 Video hướng dẫn giải Trả lời câu hỏi Hoạt động 2 trang 115 SGK Toán 9 Kết nối tri thức Xây dựng theo các bước sau để xây dựng bảng tính Excel tính toán lượng chất tan và dung môi cần thiết. Bước 1: Tạo bảng trên phần mềm Excel, điền các ô thông tin vào bảng tính.
Bước 2: Nhập số liệu vào cột nồng độ phần trăm, thể tích dung dịch, khối lượng riêng của đường (1,1 g/ml). Bước 3: Sử dụng công thức nghiệm ở HĐ 1 để nhập công thức vào cột chất tan và lượng nước cần pha. Bước 4: Hoàn thiện bảng tính: Làm tròn số liệu sau dấu phẩy một chữ số và thêm dấu phân cách hàng nghìn cho thể tích dung dịch và khối lượng. Đóng khung cho bảng Phương pháp giải: Sử dụng excel trên máy tính để tạo bảng rồi điền số liệu tương ứng. Lời giải chi tiết:
TH Video hướng dẫn giải Trả lời câu hỏi Thực hành trang 117 SGK Toán 9 Kết nối tri thức Tính số gam muối tính khiết và số gam nước tinh khiết cần thiết để có thể pha chế được 1 000 ml dung dịch nước muối sinh lí 0,9%, biết rằng khối lượng riêng của muối tinh khiết là 2,16 g/ml. Phương pháp giải: Nồng độ phần trăm C của một dung dịch tính bằng công thức \(C\% = \frac{{{m_{ct}}}}{{{m_{{\rm{dd}}}}}} \times 100\% \) Trong đó: \({m_{ct}}\) là khối lượng chất tan; \({m_{dd}}\) là khối lượng dung dịch Tính thể tích của một chất = khối lượng của chất đó : khối lượng riêng Lời giải chi tiết: Gọi số gam muối tinh khiết là x Số gam nước tinh khiết là y Nồng độ muối là 0,9% nên ta có \(\frac{x}{{x + y}}.100 = 0,9\) hay \(100x - 0,9x - 0,9y = 0\) suy ra \(99,1x - 0,9y = 0\left( 1 \right)\) Thể tích của muối là \(\frac{x}{{2,16}}\) (ml) Thể tích của nước là y ml nên thể tích của dung dịch là \(\frac{x}{{2,16}} + y = 1000\left( 2 \right)\) Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}99,1x - 0,9y = 0\\\frac{x}{{2,16}} + y = 1000\end{array} \right.\) Giải hệ ta được \(\left\{ \begin{array}{l}x \approx 9\\y \approx 995,8\end{array} \right.\) Vậy cần khoảng 9 gam muối tinh khiết và 995,8 gam nước tinh khiết
|





















Danh sách bình luận