Giải bài tập 6.5 trang 8 SGK Toán 9 tập 2 - Kết nối tri thứcBiết đường cong trong Hình 6.6 là một parabol (y = a{x^2}). a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc parabol có hoành độ (x = - 2). c) Tìm các điểm thuộc parabol có tung độ (y = 8). Quảng cáo
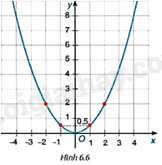
Đề bài Biết đường cong trong Hình 6.6 là một parabol \(y = a{x^2}\). a) Tìm hệ số a. b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x = - 2\). c) Tìm các điểm thuộc parabol có tung độ \(y = 8\).
Video hướng dẫn giải Phương pháp giải - Xem chi tiết a) Điểm (1; 0,5) thuộc parabol \(y = a{x^2}\) nên thay tọa độ điểm (1; 0,5) vào hàm số \(y = a{x^2}\) ta tìm được a. b) Thay \(x = - 2\) vào hàm số \(y = 0,5{x^2}\) để tìm tung độ y. c) Thay \(y = 8\) vào hàm số \(y = 0,5{x^2}\) để tìm hoành độ x. Lời giải chi tiết a) Từ đồ thị hàm số ta có, điểm (1; 0,5) thuộc parabol \(y = a{x^2}\) nên: \(0,5 = a{.1^2} \Rightarrow a = 0,5\) b) Với \(a = 0,5\) ta có: \(y = 0,5{x^2}\) Thay \(x = - 2\) vào hàm số \(y = 0,5{x^2}\) ta có: \(y = 0,5.{\left( { - 2} \right)^2} = 0,5.4 = 2\). c) Thay \(y = 8\) vào hàm số \(y = 0,5{x^2}\) ta có: \(8 = 0,5{x^2} \Rightarrow {x^2} = 16 \Rightarrow x = \pm 4\). Các điểm thuộc parabol có tung độ \(y = 8\) là: \(\left( { - 4;8} \right);\left( {4;8} \right)\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
